Matematický operátor sumácie (), aritmetická postupnosť, určovanie počtu vykonaných operácií na základe kódu v určitom programovacom jazyku.
Matematický operátor sumácie ( – Sigma)
Keďže pre spracovanie určitého objemu údajov na vstupe (zväčša uložených v množine, poli, zozname, a podobne) sa používajú v programovacích jazykoch zväčša cykly, počet operácií sa dá vyjadriť pomocou matematického operátora sumácie – .
Napríklad: znamená, že začína na čísle 1 a pokračuje po 8 (vrátane). S každou iteráciou sa sčítava časť za operátorom (v tomto prípade sa teda číslo 1 sčíta presne 8 krát: , výsledok: ).
Toto by sa dalo vyjadriť v kóde takto:
vysledok = 0
for i in range(8): # vykoná sa 8 krát
vysledok += 1
print(vysledok) # 8
Sumácia môže mať rôzny názov a definíciu riadiacej premennej, ako aj hornú hranicu. Všetky nasledujúce zápisy sú platné:
| Matematický zápis | Zápis v Python kóde |
suma = 0
for i in range(5, 10):
suma += 1
| |
suma = 0
for i in range(n+1):
suma += 1
| |
suma = 0
i = ... # napr.: môže pochádzať z vonkajšieho cyklu
for j in range(1, n+2):
suma += (i + 1)
|
Avšak, nemôžeme definovať negatívny krok. Napríklad, tento zápis nie je matematicky správny: ( by nikdy nenabudlo hodnotu 0).
Príklady pre sumáciu
Aritmetická postupnosť
Príklady vyššie sa dajú vypočítať manuálne. Ale čo ak by sme mali napríklad postupnosť 100 prvkov, napríklad: .
V tomto prípade by sa postupnosť rozbalila ako . Ručne, číslo po čísle, by sme to sčítavali asi iba dlho...
Avšak, múdri matematici si všimli, že medzi číslami platí určitý vzťah. Ak zoberieme v (rozbalenej) postupnosti vždy dva protiľahlé prvky a sčítame ich, výsledkom bude vždy rovnaké číslo. To znamená, že pre výpočet súčtu všetkých členov aritmetickej postupnosti vyššie nám stačí sčítať dva protiľahlé prvky (spravidla prvý a posledný prvok), vynásobiť ich počtom prvkov a vydeliť dvomi:
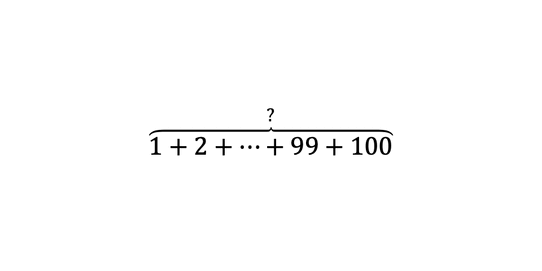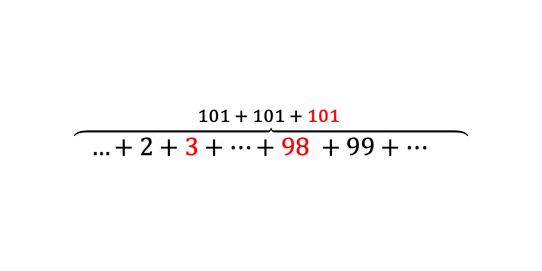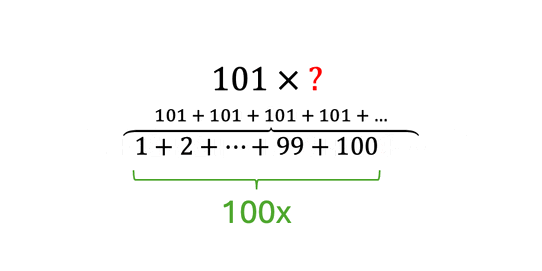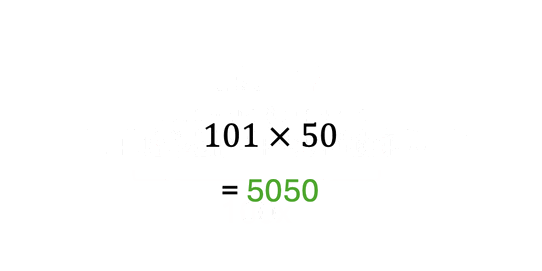
Výsledkok: . Samozrejme, je dôležité že číselný odstup od každého prvku (respektíve, súčet dvoch protiľahlých párov) je rovnaký. Napríklad, postupnosť čísiel nie je aritmetickou postupnosťou a teda by sme nemohli aplikovať metódu ktorá je znázornená vyššie.
Všeobecný vzorec pre výpočet súčtu prvkov aritmetickej postupnosti je:
Horná a dolná hranica postupnosti
Každá aritmetická postupnosť má hornú a dolnú hranicu, ktorou vyjadrujeme maximálny možný rozsah hodnôt ktoré môže postupnosť obsahovať. Spravidla:
- dolnou hranicou je prvý prvok aritmetickej postupnosti;
- hornou hranicou je posledný prvok aritmetickej postupnosti;
Počet prvkov aritmetickej postupnosti () definovanej pomocou sumácie () môžeme vypočítať ako:
(plus 1 – pretože berieme do úvahy aj prvý prvok postupnosti)
Príklady pre výpočet súčtu prvkov aritmetickej postupnosti
Určovanie počtu vykonaných operácií v kóde
Aby sme dokázali vyjadriť časovú zložitosť algoritmu, musíme spočítať operácie ktoré sa v kóde dejú – algoritmus ktorý má menší počet operácií je efektívnejší. Funkcia, ktorá udáva počet operácií v závislosti od veľkosti vstupu je definovaná matematicky ako – jej výsledná hodnota pre dané predstavuje najväčší počet operácií ktorý vykoná daný kód (pri vstupe o veľkosti ).
Inými slovami, majme napríklad tento kód pre zistenie názvu dňa podľa jeho poradia v týždni (čiže od 1 pre pondelok až po 7 pre nedeľu):
DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
# 0 1 2 3 4 5 6
poradie_v_tyzdni = 3 # tretí deň v týždni
den = DNI[poradie_v_tyzdni-1] # -1, pretože indexujeme od 0
print(den)
# "Streda" – tretím dňom v týždni je streda
Operácie ktoré kód vyššie vykonáva môžeme rozpísať a analyzovať:
DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
# alokuje sa premenná "DNI" a priradí sa jej hodnota
# z hľadiska časovej náročnosti sú konštanty O(1)
# (pretože prebehne práve 1 operácia, teda vytvorenie premennej)
poradie_v_tyzdni = 3 # toto je stále konštanta, takže O(1)
den = DNI[poradie_v_tyzdni-1] # znovu O(1)
print(den) # O(1)
Tuto sa ešte nenachádza žiadna premenná
, keďže vstup sa pre kód nikdy nemení – vždy máme pevne danú množinu v ktorej je 7 prvkov (dní) a vyberáme práve jeden, v kóde nie sú žiadne cykly ani iné vetvy).
Nezáleží na tom, koľkokrát kód vyššie spustíme, môžeme tvrdiť že vždy sa vykonajú práve 4 operácie:
- vytvorenie premennej
DNI; - vytvorenie premennej
poradie_v_tyzdni; - vytvorenie premennej
den; - výpis tejto premennej na terminál;
Teda, výsledok je (iba sčítame operácie: ). Číslo v zátvorke by predstavovalo počet operácií ktoré kód vykoná.
Ale čo ak sa vstup bude meniť? Napríklad, vo funkcii ktorá sčíta prvých
čísiel?
# premenná "n" môže byť akékoľvek prirodzené číslo
# (väčšie ako alebo rovné nule = ak na vstup nezadáme nič)
# deklarácia by mohla vyzerať napríklad takto:
# n = int(input())
def scitaj_prvych(n):
"""
Funkcia, ktorá sčíta prvých `n` čísiel a vráti výsledok sčítania.
"""
sucet = 0 # konštantné priradenie, O(1)
# toto si vysvetlíme nižšie
# (spoiler: bude nás zaujímať iba toto :))
for cislo in range(n):
sucet += cislo
return sucet # aj operácia vrátenia ("return") sa pokladá za náročnosť O(1)
Vidíme, že počet čísiel ktoré sa majú sčítať sa dynamicky menia v závislosti od toho čo zadá používateľ do terminálu (respektíve, podľa toho aké číslo je v premennej
). Z toho vyplýva, že musíme odvodiť všeobecnú rovnicu ktorá bude hovoriť, ako sa časová náročnosť kódu bude meniť v závislosti od počtu prvkov na vstupe – aspoň približne. Ak sa pozrieme na hlavný cyklus v kóde:
for cislo in range(n): # n-krát
sucet += cislo # O(1)
Teda, výsledná rovnica je:
(počet operácií súčtu je rovný počtu čísel ktoré máme sčítať)
Čo sa vlastne myslí pod pojmom "operácia"? Napríklad, kód vysledok = (1 + 2) * (2 ** 5) má hneď niekoľko operácií – je potrebné ich ďalej deliť?
Operácia je iba abstrakciou nad nejakou časťou kódu ktorá niečo robí. Môže ísť napríklad o vykonanie nejakej funkcie, priradenie premennej, aritmetickú operáciu, ale aj o porovnanie a výmenu prvkov v množine (napríklad pri algoritme Bubble sort).
Všeobecný postup pre výpočet časovej zložitosti
Všeobecný postup pre určenie časovej zložitosti by teda mohol vyzerať takto:
- Identifikovať hlavnú slučku programu ktorá spracuje údaje zo vstupu, a teda jej výkon závisí od celkového množstva údajov na vstupe (zväčša od premennej );
- Zorientovať sa, čo táto časť kódu vlastne robí a koľko údajov je vlastne potrebné spracovať. Napríklad: je potrebné prejsť všetkými údajmi na vstupe, alebo môže nastať aj prípad že slučka skončí skôr? Spracujú sa všetky údaje alebo iba polovica? A podobne...;
- Určiť časovú zložitosť operácií ktoré sú jednoznačné;
- Dať to všetko dokopy (ak je to cyklus, pravdepodobne budeme násobiť toľkokrát, koľko sa kód bude opakovať, inak sčítavame)