Greedy (pažravé) algoritmy, problém change-making (rozmenenie sumy, mincovka), divide-and-conquer (rozdeľuj a panuj), dynamické programovanie (zhora-nadol, zdola-nahor), backtracking.
Typy algoritmov a spôsoby riešenia
Existujú rôzne spôsoby riešenia algoritmických problémov. Ak máme nejaký problém ktorý sa dá riešiť algoritmicky, môžeme ho riešiť viacerými spôsobmi. Niektoré spôsoby sú už zaužívané a dajú sa použiť pre riešenie viacero typov problémov:
Greedy (pažravé) algoritmy
Podľa môjho názoru jedny z najľahšie pochopiteľných algoritmov. Ak máme nejaký problém, snažíme sa vždy vyberať tú najlepšiu variantu (môže to byť napríklad vždy najväčšie číslo). Je to zároveň algoritmus, ktorý častokrát podvedome používame v reálnom živote a možno si to ani neuvedomujeme. Napríklad, ak máme usporiadať čísla od najväčšieho po najmenšie, ako by sme postupovali inštinktívne? Pravdepodobne by sme vybrali najväčšie číslo, potom druhé najväčšie, a tak ďalej... Princíp je taký, že vždy vyberieme najväčšie číslo. A práve takto fungujú pažravé algoritmy – vždy sa snažia vybrať tú možnosť, ktorá je v aktuálnom bode riešenia problému optimálna. Avšak, nie vždy to vyústi k tomu že záverečné riešenie je optimálne.
Change-making problém
Change-making problém (taktiež nazývaný v slovenčine aj ako "mincovka") je problém, kde máme danú určitú peňažnú sumu a pre túto sumu musíme nájsť minimálny počet mincí ktoré môžeme použiť pre rozmenenie tejto sumy. Napríklad, sumu 1,23 € by sme rozmenili ako: 1 € + 0,20 € + 0,02 € + 0,01 €.
Štandardne máme v tomto probléme k dispozícií ako platidlo mince so sumami: 2 €; 1 €; 0,50 €; 0,20 €; 0,10 €; 0,05 €; 0,02 € a 0,01 €, ale problém rozmenenia sumy dokáže nájsť minimálny počet mincí pre akúkoľvek množinu hodnôt mincí (platidiel, pretože ak je hodnota vyššia tak sú to bankovky).
Tento problém sa najľahšie (a intuitívne) rieši pomocou pažravého algoritmu, preto je aj vhodný príklad pre lepšie pochopenie pažravých algoritmov: jednoducho prechádzame množinou všetkých mincí a zakaždým od sumy pre rozmenenie odčítame túto sumu. Ak sa táto suma už nevmestí (výsledok je menej ako 0), prejdeme na ďalšiu mincu. Takto pokračujeme až dokým nevyčerpáme všetky mince.
Poďme si skúsiť naprogramovať riešenie mincovky v Pythone, za pomoci pažravého algoritmu:
Riešenie mincovky sa dá aplikovať v reálnom živote v bankomatoch alebo rôznych predajných, parkovacích a iných automatoch ktoré rozmieňajú peňažné sumy.
Optimálnosť riešenia
Aj napriek tomu, že pažravé algoritmy sú z hľadiska implementácie vcelku priamočiare a jednoduché, v niektorých prípadoch nenájdu vždy optimálne riešenie.
Povedzme, že by sme mali ako platidlá zvolené neštandardné hodnoty: 6 €, 5 € a 1 €. Máme rozmeniť sumu 10 € – ako by postupoval pažravý algoritmus? Vždy by sme použili mincu s najväčšou hodnotou, takže: 6 €, potom by nasledovalo 5 €. Lenže 6 + 5 = 11 €, a to sa už do našej sumy 10 € nevmestí. Pažravý algoritmus by teda rozmenil sumu ako: 6 € + 1 € + 1 € + 1 € + 1 € = 10 €. To je správne riešenie, avšak nie je optimálne. Predsa sumu 10 € môžeme rozmeniť oveľa efektívnejšie, iba ako 5 € + 5 €!
Tu sa stretávame s neoptimálnym algoritmom. Nie je garantované, že pažravý algoritmus nájde vždy optimálne riešenie (v niektorých prípadoch môžu byť vstupné hodnoty zadané tak, že algoritmus sa náhodou trafí a vráti optimálne riešenie, ale to nie je garantované).
Naopak, optimálne algoritmy prehľadávajú všetky možnosti tak, aby vrátili vždy optimálne riešenie (za cenu toho, že môžu byť časovo viacej náročné, keďže pracujú neintuitívne a musia prehľadať všetky alternatívy v ktorých by mohlo byť skryté správne riešenie). Pri voľbe vhodného algoritmu pre náš prípad použitia musíme tiež dbať na to, či je garantované že nájdu optimálne riešenie. Inými slovami, musíme voliť medzi rýchlosťou vs. presnosťou ktoré nám ponúkajú rôzne algoritmy.
Divide-and-conquer (rozdeľuj a panuj)
Pri tomto type algoritmov sa jeden problém rozdelí na viacero menších problémov ktoré sa riešia nezávisle od seba a potom sa spoja do záverečného riešenia. Typickým príkladom je algoritmus merge-sort, ktorý pole rozdeľuje postupne na polovicu a na konci sa všetky polia zlučujú do jedného zoradeného poľa.
Metóda "rozdeľuj a panuj" má tri hlavné fázy:
- Rozdeľuj (divide) – problém sa delí na menšie, nezávislé celky;
- Rieš (solve) – fáza riešenia problému rieši každý problém nezávisle;
- Panuj (conquer) – čiastkové riešenia sa spoja do jedného finálneho riešenia;
Triediace algoritmy riešené metódou "rozdeľuj a panuj" (merge-sort, quick-sort) majú zväčša logaritmickú výpočtovú zložitosť – čo je lepšie ako priame metódy so zložitosťou (logaritmická výpočtová zložitosť je typická pre riešenia problémov, ktoré delia vstup s každou iteráciou alebo rekurzívnym volaním na polovicu).
Dynamické programovanie
Rekurzívne algoritmy (ako napríklad "rozdeľuj a panuj") sú optimálnejšie ako priame algoritmy, avšak majú nevýhodu – ak voláme rekurzívnu funkciu s rovnakými parametrami (teda ak predpokladáme že funkcia má pre rovnaký vstup vrátiť rovnaký výstup), tak sa výsledok musí znovu vypočítať, čo vedie k exponenciálnej časovej zložitosti. Je to veľmi nevýhodné pre riešenie algoritmov, kde problémy závisia od iných čiastkových riešení a pod-problémov.
Riešením je použitie dynamického programovania. Dynamické programovanie používa optimalizačnú techniku, ktorá sa nazýva memoizácia - memoizovaná funkcia ukladá výsledky predošlých volaní, a ak je funkcia znova volaná s rovnakými parametrami, tak funkcia vráti už uložený výsledok (namiesto toho aby funkcia hodnotu výsledku znovu prepočítavala). Táto optimalizácia môže drasticky redukovať čas potrebný pre výpočet konečného výsledku.
Existuje niekoľko typov dynamického programovania, v závislosti od typu problému a dátovej štruktúry pre ukladanie medzivýsledkov:
- 1-dimenzionálne dynamické programovanie (1D DP; lineárne stavy) – používa pole, kde indexom je vstupná hodnota a hodnota na tom indexe je uložený výsledok pre tú hodnotu. Napríklad, pole pre ukladanie čísiel Fibonacciho postupnosti, kde indexom je poradie čísla v postupnosti () a hodnota na tom indexe je konkrétne číslo v postupnosti:
dp = [0, 1, 1, 2, 3, 5, 8, 13, ...] - 2-dimenzionálne dynamické programovanie (2D DP; páry hodnôt) – 2D pole (pole v poli), ktoré uchováva hodnoty pre páry hodnôt, napríklad problém najdlhšieho palindromického podreťazca.
- 3 a viac-dimenzionálne dynamické programovanie (3D DP, 4D DP...; trojice, štvorice... hodnôt) – 3 a viac-dimenzionálne polia (vnorené polia).
- Rozsahové dynamické programovanie (interval DP; pracuje s hodnotami ktoré majú určitý rozsah, napríklad množiny alebo reťazce).
Dynamické programovanie zhora-nadol
Pri dynamickom programovaní zhora-nadol používame rekurziu. Začíname od vrcholu a postupne sa vnárame do rekurzie, až pokým úplne dole nenarazíme na triviálny prípad.
Fibonacciho postupnosť (s memoizáciou)
Fibonacciho postupnosť je typickým príkladom rekurzie, kde riešenie závisia navzájom od seba. Fibonacciho postupnosť je daná rekurzívnym vzorcom:
Triviálne prípady sú pre a pre . Ak chceme vypočítať -té číslo v tejto postupnosti, musíme sčítať výsledky dvoch predošlých volaní, a tie volania musia vypočítať ďalšie dve predtým, a tak ďalej... Každé volanie pritom začína výpočet odznova, pretože problémy sú riešené nezávisle, čo vedie k tomu že výpočty sa opakujú. Napríklad, pre :
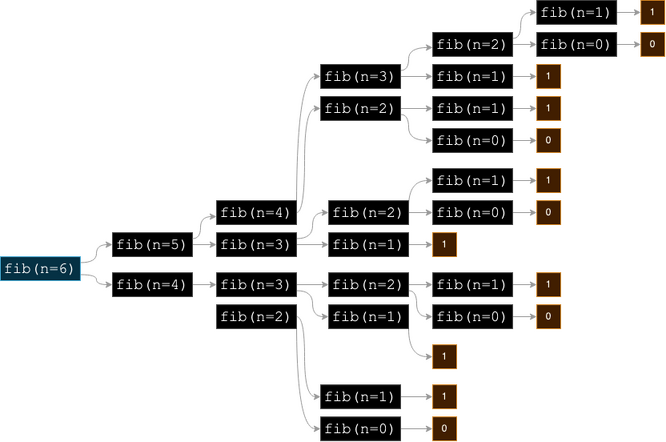
Vidíme, že v tomto strome sa veľa výpočtov opakuje – každý výpočet vytvorí ďalšie a ďalšie vetvy a rekurzívnych volaní je veľmi veľa.
Cieľom dynamického programovania je rekurziu obmedziť tak, že si vytvoríme premennú s tabuľkou pre medzivýsledky a ak zavoláme funkciu s parametrami pre ktoré máme uložený výsledok, tak sa nevnárame ďalej do rekurzie ale iba vrátime tento výsledok.
Skúsme upraviť rekurzívny výpočet Fibonacciho postupnosti tak, aby používala dynamické programovanie (DP) s tabuľkou pre memoizáciu:
Dynamické programovanie zdola-nahor
Tento typ dynamického programovania nepoužíva rekurziu, ale cykly. Počas prechodu cyklom sa postupne vypĺňa tabuľka s medzivýsledkami. Pri počítaní vyšších a vyšších hodnôt sa zoberú predošlé výsledky z tabuľky, ak v nej existujú – preto sa to nazýva programovanie zdola-nahor (od menších hodnôt po vyššie).
Backtracking
Metóda backtracking prehľadáva všetky možné riešenia a nakoniec vyberie to najoptimálnejšie. Pri výpočte sa vyberie jedna cesta – ak nás výsledok privedie bližšie k nášmu cieľu, pokračujeme. Ak nie (alebo narazíme na slepú uličku), tak sa vrátime o krok späť (to predstavuje backtracking) a skúsime ísť inou cestou. Na konci je výsledkom vždy najoptimálnejšie riešenie. Avšak, backtrackingové algoritmy majú obyčajne exponenciálnu výpočtovú zložitosť (pretože musíme prehľadať všetky možné kombinácie výsledkov, a počet kombinácií predstavuje umocnenie).
Problém batoha (knapsack problem)
Predstavme si, že ideme na výlet do hôr. Máme batoh s určitou maximálnou nosnosťou a nejaké veci, ktoré môžeme do batohu zbaliť. Každá vec má určitú hmotnosť a hodnotu (môže to byť napríklad úžitková hodnota, ako veľmi túto vec preferujeme nad ostatnými, ako veľmi ju potrebujeme, a podobne...). Otázkou je, ako zbaliť veci tak aby sme batoh naplnili čo najviac (nepresiahli jeho maximálnu nosnosť) a zároveň aby súčet hodnôt týchto vecí bol čo najvyšší.
Tento algoritmus môže mať viacero formulácií, my máme namysli verziu knapsack 0/1 (to znamená, že neberieme do úvahy čiastkové hodnoty – inými slovami, buď danú vec nezoberieme vôbec alebo ju zoberieme celú).