Určovanie počtu operácií

Matematický operátor sumácie ($\sum$), aritmetická postupnosť, určovanie počtu vykonaných operácií na základe kódu v určitom programovacom jazyku.

Rýchlokurz matematickej časti

Matematický operátor sumácie ($\sum$ – Sigma)

Keďže pre spracovanie určitého objemu údajov na vstupe (zväčša uložených v množine, poli, zozname, a podobne) sa používajú v programovacích jazykoch zväčša cykly, počet operácií sa dá vyjadriť pomocou matematického operátora sumácie – $\sum$.

Napríklad: $\sum _{i=1}^{8}1$ znamená, že $i$ začína na čísle 1 a pokračuje po 8 (vrátane). S každou iteráciou sa sčítava časť za operátorom (v tomto prípade sa teda číslo 1 sčíta presne 8 krát: $\stackrel{8}{\overbrace{1+1+1+1+1+1+1+1}}$, výsledok: $\sum _{i=1}^{8}1=8$).

Toto by sa dalo vyjadriť v kóde takto:

vysledok = 0
for i in range(8):  # vykoná sa 8 krát
    vysledok += 1
print(vysledok)  # 8

Sumácia môže mať rôzny názov a definíciu riadiacej premennej, ako aj hornú hranicu. Všetky nasledujúce zápisy sú platné:

Matematický zápis	Zápis v Python kóde
$\sum _{i=5}^{9}1$	suma = 0 for i in range(5, 10): suma += 1
$\sum _{i=0}^{n}1$	suma = 0 for i in range(n+1): suma += 1
$\sum _{j=1}^{n+1}(i+1)$	suma = 0 i = ... # napr.: môže pochádzať z vonkajšieho cyklu for j in range(1, n+2): suma += (i + 1)

Avšak, nemôžeme definovať negatívny krok. Napríklad, tento zápis nie je matematicky správny: $\sum _{j=10}^{0}1$ ($j$ by nikdy nenabudlo hodnotu 0).

Príklady pre sumáciu:

1

$\sum _{i=1}^{8}1$ =

2

$\sum _{i=1}^{5}7$ =

3

$\sum _{i=1}^{5}i$ =

Aritmetická postupnosť

Príklady vyššie sa dajú vypočítať manuálne. Ale čo ak by sme mali napríklad postupnosť 100 prvkov, napríklad: $\sum _{i=1}^{100}i$.

V tomto prípade by sa postupnosť rozbalila ako $\stackrel{?}{\overbrace{1+2+\cdots +99+100}}$. Ručne, číslo po čísle, by sme to sčítavali asi iba dlho...

Avšak, múdri matematici si všimli, že medzi číslami platí určitý vzťah. Ak zoberieme v (rozbalenej) postupnosti vždy dva protiľahlé prvky a sčítame ich, výsledkom bude vždy rovnaké číslo. To znamená, že pre výpočet súčtu všetkých členov aritmetickej postupnosti vyššie nám stačí sčítať dva protiľahlé prvky (spravidla prvý a posledný prvok), vynásobiť ich počtom prvkov a vydeliť dvomi:

Výpočet súčtu prvých 100 prvkov aritmetickej postupnosti.

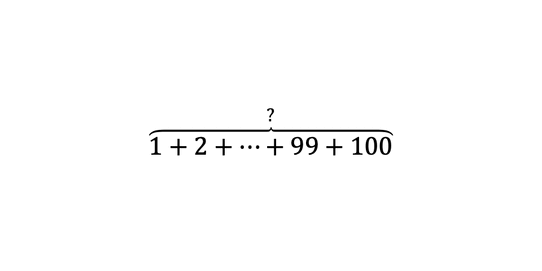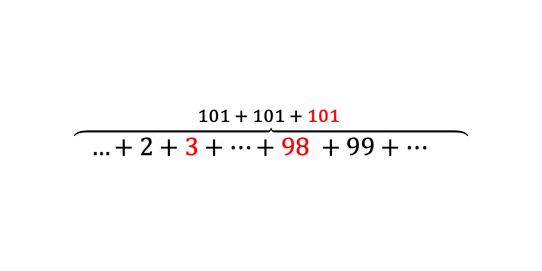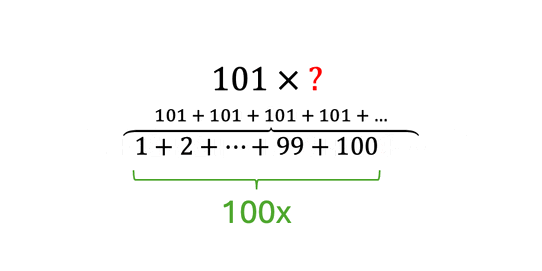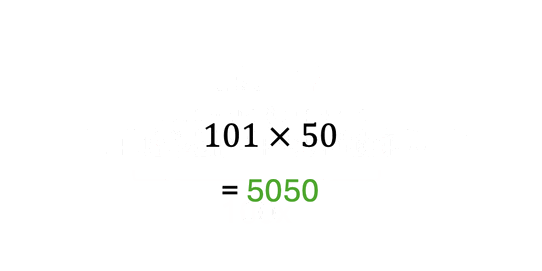
Výsledok: $\sum _{i=1}^{100}i=50\times 101=5050$. Samozrejme, je dôležité že číselný odstup od každého prvku (respektíve, súčet dvoch protiľahlých párov) je rovnaký. Napríklad, postupnosť čísiel $1,3,5,7,11,\cdots$ nie je aritmetickou postupnosťou a teda by sme nemohli aplikovať metódu ktorá je znázornená vyššie.

Všeobecný vzorec pre výpočet súčtu $n$ prvkov aritmetickej postupnosti je:

$$\begin{array}{rl}{S}_n& =\frac{(a_1+a_n)\times n}{2}\\ \text{kde: }{a}_1& \text{ je prvý prvok (prvok na pozícií 1) }\\ a_n& \text{ je posledný prvok (na pozícií n) }\\ n& \text{ je počet prvkov }\\ \end{array}$$

Horná a dolná hranica postupnosti

Každá aritmetická postupnosť má hornú a dolnú hranicu, ktorou vyjadrujeme maximálny možný rozsah hodnôt ktoré môže postupnosť obsahovať. Spravidla:

• dolnou hranicou je prvý prvok aritmetickej postupnosti;
• hornou hranicou je posledný prvok aritmetickej postupnosti;

Počet prvkov aritmetickej postupnosti ($n$) definovanej pomocou sumácie ($\sum _{\text{i = (dolná hranica)}}^{\text{(horná hranica)}}$) môžeme vypočítať ako:

$$\text{(horná hranica)}-\text{(dolná hranica)}+1$$

(plus 1 – pretože berieme do úvahy aj prvý prvok postupnosti)

Príklady pre výpočet súčtu prvkov aritmetickej postupnosti:

1

$\sum _{i=1}^{300}i$ =

2

$\sum _{i=10}^{100}i$ =

3

$\sum _{k=24}^{365}i$ =

Určovanie počtu vykonaných operácií v kóde

Poďme ale začať pekne od začiatku a krok po kroku. Začneme jednoduchými príkladmi a postupne budeme zvyšovať náročnosť.

Majme napríklad tento kód pre zistenie názvu dňa podľa jeho poradia v týždni (čiže od 1 pre pondelok až po 7 pre nedeľu):

DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
#           0         1          2         3         4         5          6

poradie_v_tyzdni = 3          # tretí deň v týždni
den = DNI[poradie_v_tyzdni-1] # -1, pretože indexujeme od 0

print(den)
# "Streda" – tretím dňom v týždni je streda

Tuto sa ešte nenachádza žiadna premenná $n$, keďže vstup sa pre kód nikdy nemení – vždy máme pevne danú množinu v ktorej je 7 prvkov (dní) a vyberáme práve jeden, v kóde nie sú žiadne cykly ani iné vetvy).

Nezáleží na tom, koľkokrát kód vyššie spustíme, môžeme tvrdiť že vždy sa vykonajú práve 4 operácie:

1. vytvorenie premennej DNI;
2. vytvorenie premennej poradie_v_tyzdni;
3. vytvorenie premennej den;
4. výpis tejto premennej na terminál;

Teda, $T=4$.

🤔

Čo sa vlastne myslí pod pojmom "operácia"? Napríklad, kód vysledok = (1 + 2) * (2 ** 5) má hneď niekoľko operácií – je potrebné ich ďalej deliť?

Operácia je iba abstrakciou nad nejakou časťou kódu ktorá niečo robí. Môže ísť napríklad o vykonanie nejakej funkcie, priradenie premennej, ale aj o porovnanie a výmenu prvkov v množine (napríklad pri algoritme Bubble sort).

Operácia vyššie síce vykonáva viacero aritmetických operácií (sčítanie, umocnenie, vynásobenie), ale rátame ju iba ako jednu operáciu. Je to z toho dôvodu, že nikdy nemôžeme presne určiť časovú zložitosť algoritmu (rôzne procesory a architektúry majú rôznu rýchlosť, a tak ďalej), vnímame to na vyššej abstraktnej úrovni. Väčšinou sa jedna operácia berie ako jeden riadok kódu ktorý niečo robí.

Určovanie počtu operácií v kóde pre rôzne veľkosti vstupu $n$

Aby sme dokázali vyjadriť časovú zložitosť algoritmu, musíme všeobecne vyjadriť funkciu pre zistenie počtu operácií pre dané $n$ (veľkosť vstupu) – algoritmus ktorý má menší počet operácií je efektívnejší. Funkcia, ktorá udáva počet operácií v závislosti od veľkosti vstupu je definovaná matematicky ako $T(n)$. Jej výsledná hodnota pre dané $n$ predstavuje najväčší počet operácií ktorý vykoná daný kód (pri vstupe o veľkosti $n$).

Pri týchto typoch úloh máme zadaný konkrétny kód v nejakom programovacom jazyku (napríklad v Pythone) a musíme určiť funkciu $T(n)$. Kľúčom je prepísať si kód na matematický zápis ktorý vyjadruje počet operácií a potom to čo najviac zjednodušiť a zovšeobecniť (aby sme tam mali nanajvýš iba premennú $n$, bez žiadnych riadiacich premenných ako $i$, $j$, $k$ a podobne).

Majme kód v Pythone. Chceme vyjadriť funkciu $T(n)$ pre počet výpisov:

for i in range(n):
  print("*", end="")

Už vieme, že print má konštantnú časovú zložitosť (tvárime sa, že je to jedna operácia v kóde, teda akoby číslo 1). Matematicky môžeme teda cyklus vyššie vyjadriť ako: $T(n)=\sum _{i=0}^{n-1}1$.

Využívame pritom vlastnosti funkcie range – začíname od čísla 0 a ideme až pokým nedosiahneme číslo $n$ (ktoré ale už v cykle nie je zahrnuté, pretože range vynecháva posledný prvok: range(3) => [0, 1, 2] # spolu tri prvky, ale bez 3). Dostali sme matematický zápis aritmetickej postupnosti, ktorú už vieme vyjadriť:

$T(n)=\sum _{i=0}^{n-1}1=1\times (n-1-0+1)$

Prečo: vieme, že horná hranica je $n-1$ a dolná hranica je $0$. Počet prvkov (jednotiek) teda získame ako: $\text{horná hranica}-\text{dolná hranica}+1$. Potom iba spočítame, koľkokrát sa tam nachádza číslo jedna (toľkokrát, koľko je tam prvkov, keďže všetky prvky sú 1). Teda, $1\times (n-1-0+1)$.

Po zjednodušení je konečný výsledok: $T(n)=n$. Hmm, kto by povedal že takýto kód bude volať print presne n-krát 😱? Ale aspoň sme dokázali, že naše matematické metódy fungujú...

Teraz skúsime niečo iné:

for i in range(1, 2 * n):
  print("*")
  print(".")

Úlohou je (opäť) zistiť počet volaní na funkciu print (vyjadriť to všeobecne ako matematickú funkciu časovej zložitosti – $T(n)$). Máme jeden cyklus s dvomi volaniami na print. Tento cyklus generuje čísla od 1 po 2 * n. Keďže jazyk Python nezahŕňa hornú hranicu do čísiel ktoré generuje, cyklus sa zastaví na čísle (2 * n) - 1. No a dva printy v cykle iba znamenajú, že sčítavame dve operácie (dve jednotky) – sčítavanie robíme vždy ak máme za sebou sekvenciu operácií na rovnakej úrovni odsadenia. Matematicky vieme cyklus vyššie zapísať ako:

$$\sum _{i=1}^{2n-1}(1+1)$$

Určíme počet prvkov: $\text{horná hranica}-\text{dolná hranica}+1=(2n-1)\cancel{-1}\cancel{+1}=2n-1$.

To znamená, že počet $(1+1)$ v cykle je $2n-1$. Výsledok je teda:

$$\begin{array}{rl}T(n)& =(1+1)\times (2n-1)\\ & =2\times (2n-1)\\ & =\stackrel{4n}{\overbrace{(2\times 2n)}}+\stackrel{-2}{\overbrace{(2\times \text{-1})}}\\ T(n)& =4n-2\\ \end{array}$$

Skúsme ešte niečo ťažšie. Určme počet výpisov (volaní na print) pre nasledovný kód:

for i in range(1, n):
  print(i + n)

  for j in range(n-2):
    for k in range(n-2):
      print((i * n + j) * n + k)

    print(j * 2)

Na prvý pohľad sa to môže zdať zložité, pretože používame v printoch viacero premenných. Avšak, zaujíma nás iba počet volaní na print, nie konkrétne hodnoty ktoré sa vypíšu. Teda, nemusíme vôbec brať do úvahy čo sa v printoch nachádza.

Máme 3 cykly ktoré sú vnorené, pritom každý z nich realizuje jeden print. Keďže sekvenčné operácie sa sčítavajú a sčítavanie je kumulatívna operácia (nezáleží v akom poradí sčítavame, výsledok je rovnaký), môžeme si kód predstaviť zjednodušene. Ak k tomu ešte pridáme fakt že nás nezaujíma obsah printov, tak z hľadiska analýzy počtu operácií je tento kód identický s kódom vyššie:

for i in range(1, n):  # 1. cyklus
  print(1)
# +
  for j in range(n-2):  # 2. cyklus
    print(1)
#   +
    for k in range(n-2):  # 3. cyklus
      print(1)

To už vyzerá trochu jednoduchšie. Matematicky to môžeme zapísať ako:

$$T(n)=\stackrel{\text{1. cyklus}}{\overbrace{\sum _{i=1}^{(n)-1}}}(1+\stackrel{\text{2. cyklus}}{\overbrace{\sum _{j=0}^{(n-2)-1}}}(1+\stackrel{\text{3. cyklus}}{\overbrace{\sum _{k=0}^{(n-2)-1}}}(1)))$$

V hornej hranici nesmieme zabudnúť pridať -1, pretože Python nezahŕňa túto hodnotu v range (ako už vieme, cyklus skončí pri predposlednej hodnote). Ak máme viacero vnorených cyklov, začíname vždy od cyklu ktorý je najviac vnorený (pamätajme si, že počet prvkov sa vypočíta ako $\text{horná hranica}-\text{dolná hranica}+1$):

$\begin{array}{rl}\sum _{k=0}^{n-3}(1)& =1\times \stackrel{\text{počet prvkov}}{\overbrace{(n-3\cancel{-0}+1)}}\\ & =n-2\\ \end{array}$

Hodnotu z cyklu na tretej úrovni dosadíme do druhého cyklu:

$\begin{array}{rl}\sum _{k=0}^{n-3}(1+\stackrel{\text{3. cyklus}}{\overbrace{(n-2)}})& =(1+(n-2))\times \stackrel{\text{počet prvkov v 2. cykle}}{\overbrace{(n-3\cancel{-0}+1)}}\\ & =(1+n-2)\times (n-2)\\ & =(n-1)\times (n-2)\\ & =n^2-2n-n+2\\ & =n^2-3n+2\end{array}$

Nakoniec iba dopočítame vonkajší cyklus:

$\begin{array}{rl}T(n)& =\sum _{i=1}^{n-1}(1+\stackrel{\text{2. cyklus}}{\overbrace{n^2-3n+2}})\\ & =(n^2-3n+3)\times (n-1\cancel{-1+1})\\ & =n^2\times (n-1)-3n\times (n-1)+3\times (n-1)\\ & =(n^3-n^2)-(3n^2+3n)+(3n-3)\\ T(n)& =n^3-4n^2+6n-3\end{array}$

Teda, počet operácií pre kód vyššie je daný funkciou $T(n)=n^3-4n^2+6n-3$ (kde $n$ je veľkosť vstupu – číslo ≥ 1).

Riešenie môžeme overiť pre niekoľko vstupov, ak do kódu doplníme premennú ktorú budeme navyšovať pri každom volaní na print:

vstupy = range(2, 7)

for n in vstupy:
  pocet_printov = 0

  # --------------------------- #
  for i in range(1, n):
    # print(1)
    pocet_printov += 1

    for j in range(n - 2):
      # print(1)
      pocet_printov += 1

      for k in range(n - 2):
        # print(1)
        pocet_printov += 1
  # --------------------------- #

  # naša funkcia `T(n)`:
  ocakavany_pocet = (n**3) - 4*(n**2) + (6*n) - 3

  print("pre n =", n)
  print("očakávaný počet printov:", ocakavany_pocet)
  print("skutočný počet printov:", pocet_printov)
  print()

Po spustení vidíme, že očakávaný počet operácií sa zhoduje so skutočným počtom, riešenie je teda správne (pre veľkosti vstupov n od 2 po 6):

pre n = 2
očakávaný počet printov: 1
skutočný počet printov: 1

pre n = 3
očakávaný počet printov: 6
skutočný počet printov: 6

pre n = 4
očakávaný počet printov: 21
skutočný počet printov: 21

pre n = 5
očakávaný počet printov: 52
skutočný počet printov: 52

pre n = 6
očakávaný počet printov: 105
skutočný počet printov: 105

Určovanie počtu operácií v kóde pre rôzne veľkosti vstupu $n$ (s riadiacimi premennými)

Častokrát sa stane, že počas cyklu používame aj riadiacu premennú (napríklad $i$) ktorá mení svoju hodnotu s každou iteráciou. Určenie funkcie $T(n)$ môže byť pre takéto cykly zložité, pretože nemôžme jednoznačne určiť akú hodnotu bude mať $i$ (na rozdiel od $n$ ktoré sa nemení).

Majme napríklad cyklus $\sum _{i=1}^{n}i$. Všeobecne je to jednoducho $n\times i$, avšak my odtiaľ potrebujeme dať preč premennú $i$ (pretože sa mení s každou iteráciou, a napokon, funkcia $T(n)$ ani neobsahuje miesto pre ďalší parameter kam by sa $i$ zmestilo).

Keď nevieme, ako sa pohnúť ďalej tak je dobré si cyklus rozpísať s konkrétnymi číslami namiesto $i$ (objaví sa nám vzor, podľa ktorého dokážeme identifikovať vzťahy medzi jednotlivými iteráciami a odvodiť všeobecný vzorec). Teda, cyklus vyššie je v podstate:

$$\sum _{i=1}^{n}i=1+2+3+\cdots +(n-1)+n$$

Prvým prvkom je vždy číslo 1 (pretože tak je to definované pod sumou: $i=1$) a posledným prvkom je $n$ (čo vidíme hore). Počet prvkov vieme zistiť pomocou vzorca: $\text{(horná hranica)}-\text{(dolná hranica)}+1=n-1+1=n\text{ prvkov}$ (je to očividné, avšak tento vzorec pomôže v prípade ak cyklus začína od čísla iného ako 1, aby sme sa zbytočne nepomýlili).

Ak máme tieto informácie, vieme ich vložiť do vzorca pre výpočet súčtu $n$ prvkov aritmetickej postupnosti a získame funkciu $T(n)$:

$$\begin{array}{rl}{S}_n& =\frac{(a_1+a_n)\times n}{2}\\ T(n)& =\frac{(1+n)\times n}{2}\\ & =\frac{(n^2+n)}{2}\\ \end{array}$$

Výsledok: počet operácií pre ľubovoľnú veľkosť vstupu $n$ môžeme určiť ako $T(n)=\frac{(n^2+n)}{2}$.

Pri takomto type úloh sa treba zamyslieť, že keď čísla rozpisujeme, tak namiesto troch bodiek tam môže byť akákoľvek veľká postupnosť čísiel – preto rozpíšeme iba zopár, aby sme lepšie videli vzory ktoré sa opakujú a vedeli pre ne odvodiť všeobecnú funkciu. Zameriavame sa na to, o aký typ postupnosti sa jedná (aritmetická/geometrická – o tej bude reč v ďalšej téme), ktorý prvok je prvý a ktorý posledný a koľko je prvkov spolu.

Presuňme sa na analýzu konkrétnych zdrojových kódov. Majme napríklad:

n = int(input("n: "))
op = 0

for i in range(n):
  for j in range(i):
    op += 1

print(op)

Cieľom je určiť, koľkokrát sa zrealizuje súčet (respektíve, koľkokrát sa vykoná riadok číslo 6).

Prepíšeme cyklus (riadok 4 až 6) na matematický zápis (nesmieme zabudnúť od hornej hranici odpočítať 1!):

$$T(n)=\sum _{i=0}^{n-1}\left(\sum _{j=0}^{i-1}1\right)$$

.

« Úvod do výpočtovej zložitosti

Určovanie počtu operácií v rekurzívnych volaniach »