Určovanie počtu operácií

Matematický operátor sumácie ($\sum$), aritmetická postupnosť, určovanie počtu vykonaných operácií na základe kódu v určitom programovacom jazyku.

Matematický operátor sumácie ($\sum$ – Sigma)

Keďže pre spracovanie určitého objemu údajov na vstupe (zväčša uložených v množine, poli, zozname, a podobne) sa používajú v programovacích jazykoch zväčša cykly, počet operácií sa dá vyjadriť pomocou matematického operátora sumácie – $\sum$.

Napríklad: $\sum _{i=1}^{8}1$ znamená, že $i$ začína na čísle 1 a pokračuje po 8 (vrátane). S každou iteráciou sa sčítava časť za operátorom (v tomto prípade sa teda číslo 1 sčíta presne 8 krát: $\stackrel{8}{\overbrace{1+1+1+1+1+1+1+1}}$, výsledok: $\sum _{i=1}^{8}1=8$).

Toto by sa dalo vyjadriť v kóde takto:

vysledok = 0
for i in range(8):  # vykoná sa 8 krát
    vysledok += 1
print(vysledok)  # 8

Sumácia môže mať rôzny názov a definíciu riadiacej premennej, ako aj hornú hranicu. Všetky nasledujúce zápisy sú platné:

Matematický zápis	Zápis v Python kóde
$\sum _{i=5}^{9}1$	suma = 0 for i in range(5, 10): suma += 1
$\sum _{i=0}^{n}1$	suma = 0 for i in range(n+1): suma += 1
$\sum _{j=1}^{n+1}(i+1)$	suma = 0 i = ... # napr.: môže pochádzať z vonkajšieho cyklu for j in range(1, n+2): suma += (i + 1)

Avšak, nemôžeme definovať negatívny krok. Napríklad, tento zápis nie je matematicky správny: $\sum _{j=10}^{0}1$ ($j$ by nikdy nenabudlo hodnotu 0).

Príklady pre sumáciu:

1

$\sum _{i=1}^{8}1$ =

2

$\sum _{i=1}^{5}7$ =

3

$\sum _{i=1}^{5}i$ =

Aritmetická postupnosť

Príklady vyššie sa dajú vypočítať manuálne. Ale čo ak by sme mali napríklad postupnosť 100 prvkov, napríklad: $\sum _{i=1}^{100}i$.

V tomto prípade by sa postupnosť rozbalila ako $\stackrel{?}{\overbrace{1+2+\cdots +99+100}}$. Ručne, číslo po čísle, by sme to sčítavali asi iba dlho...

Avšak, múdri matematici si všimli, že medzi číslami platí určitý vzťah. Ak zoberieme v (rozbalenej) postupnosti vždy dva protiľahlé prvky a sčítame ich, výsledkom bude vždy rovnaké číslo. To znamená, že pre výpočet súčtu všetkých členov aritmetickej postupnosti vyššie nám stačí sčítať dva protiľahlé prvky (spravidla prvý a posledný prvok), vynásobiť ich počtom prvkov a vydeliť dvomi:

Výpočet súčtu prvých 100 prvkov aritmetickej postupnosti.

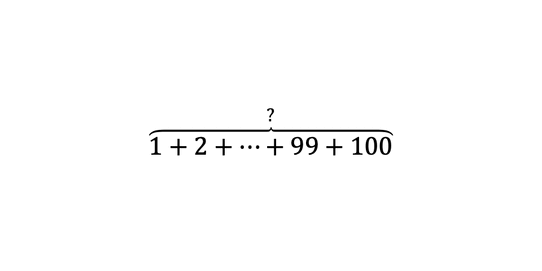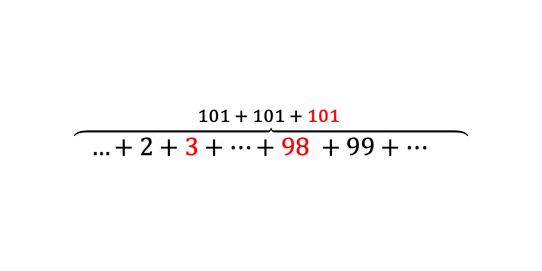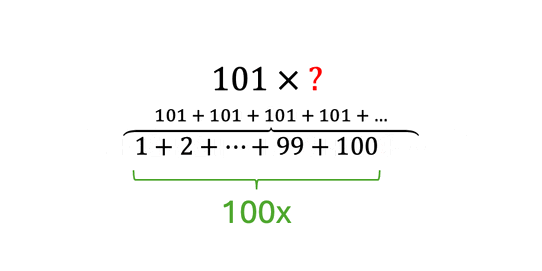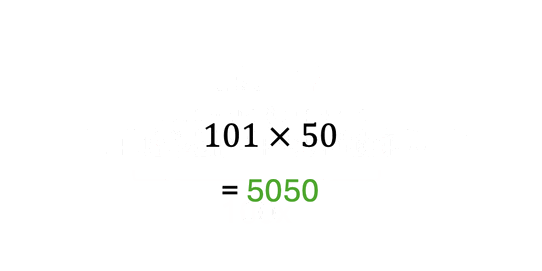
Výsledkok: $\sum _{i=1}^{100}i=50\times 101=5050$. Samozrejme, je dôležité že číselný odstup od každého prvku (respektíve, súčet dvoch protiľahlých párov) je rovnaký. Napríklad, postupnosť čísiel $1,3,5,7,11,\cdots$ nie je aritmetickou postupnosťou a teda by sme nemohli aplikovať metódu ktorá je znázornená vyššie.

Všeobecný vzorec pre výpočet súčtu $n$ prvkov aritmetickej postupnosti je:

$$\begin{array}{rl}{S}_n& =\frac{(a_1+a_n)\times n}{2}\\ \text{kde: }{a}_1& \text{ je prvý prvok (prvok na pozícií 1) }\\ a_n& \text{ je posledný prvok (na pozícií n) }\\ n& \text{ je počet prvkov }\\ \end{array}$$

Horná a dolná hranica postupnosti

Každá aritmetická postupnosť má hornú a dolnú hranicu, ktorou vyjadrujeme maximálny možný rozsah hodnôt ktoré môže postupnosť obsahovať. Spravidla:

• dolnou hranicou je prvý prvok aritmetickej postupnosti;
• hornou hranicou je posledný prvok aritmetickej postupnosti;

Počet prvkov aritmetickej postupnosti ($n$) definovanej pomocou sumácie ($\sum _{\text{i = (dolná hranica)}}^{\text{(horná hranica)}}$) môžeme vypočítať ako:

$$\text{(horná hranica)}-\text{(dolná hranica)}+1$$

(plus 1 – pretože berieme do úvahy aj prvý prvok postupnosti)

Príklady pre výpočet súčtu prvkov aritmetickej postupnosti:

1

$\sum _{i=1}^{300}i$ =

2

$\sum _{i=10}^{100}i$ =

3

$\sum _{k=24}^{365}i$ =

Určovanie počtu vykonaných operácií v kóde

Aby sme dokázali vyjadriť časovú zložitosť algoritmu, musíme spočítať operácie ktoré sa v kóde dejú – algoritmus ktorý má menší počet operácií je efektívnejší. Funkcia, ktorá udáva počet operácií v závislosti od veľkosti vstupu je definovaná matematicky ako $T(n)$ – jej výsledná hodnota pre dané $n$ predstavuje najväčší počet operácií ktorý vykoná daný kód (pri vstupe o veľkosti $n$).

Inými slovami, majme napríklad tento kód pre zistenie názvu dňa podľa jeho poradia v týždni (čiže od 1 pre pondelok až po 7 pre nedeľu):

DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
#           0         1          2         3         4         5          6

poradie_v_tyzdni = 3          # tretí deň v týždni
den = DNI[poradie_v_tyzdni-1] # -1, pretože indexujeme od 0

print(den)
# "Streda" – tretím dňom v týždni je streda

Operácie ktoré kód vyššie vykonáva môžeme rozpísať a analyzovať:

DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
# alokuje sa premenná "DNI" a priradí sa jej hodnota
# z hľadiska časovej náročnosti sú konštanty O(1)
# (pretože prebehne práve 1 operácia, teda vytvorenie premennej)

poradie_v_tyzdni = 3 # toto je stále konštanta, takže O(1)
den = DNI[poradie_v_tyzdni-1] # znovu O(1)
print(den) # O(1)

Tuto sa ešte nenachádza žiadna premenná $n$, keďže vstup sa pre kód nikdy nemení – vždy máme pevne danú množinu v ktorej je 7 prvkov (dní) a vyberáme práve jeden, v kóde nie sú žiadne cykly ani iné vetvy).

Nezáleží na tom, koľkokrát kód vyššie spustíme, môžeme tvrdiť že vždy sa vykonajú práve 4 operácie:

1. vytvorenie premennej DNI;
2. vytvorenie premennej poradie_v_tyzdni;
3. vytvorenie premennej den;
4. výpis tejto premennej na terminál;

Teda, výsledok je $T(n)=4$ (iba sčítame operácie: $1+1+1+1$). Číslo v zátvorke by predstavovalo počet operácií ktoré kód vykoná.

Ale čo ak sa vstup bude meniť? Napríklad, vo funkcii ktorá sčíta prvých $n$ čísiel?

# premenná "n" môže byť akékoľvek prirodzené číslo
# (väčšie ako alebo rovné nule = ak na vstup nezadáme nič)
# deklarácia by mohla vyzerať napríklad takto:
#  n = int(input())

def scitaj_prvych(n):
  """
  Funkcia, ktorá sčíta prvých `n` čísiel a vráti výsledok sčítania.
  """

  sucet = 0 # konštantné priradenie, O(1)

  # toto si vysvetlíme nižšie
  # (spoiler: bude nás zaujímať iba toto :))
  for cislo in range(n):
    sucet += cislo

  return sucet # aj operácia vrátenia ("return") sa pokladá za náročnosť O(1)

Vidíme, že počet čísiel ktoré sa majú sčítať sa dynamicky menia v závislosti od toho čo zadá používateľ do terminálu (respektíve, podľa toho aké číslo je v premennej $n$). Z toho vyplýva, že musíme odvodiť všeobecnú rovnicu ktorá bude hovoriť, ako sa časová náročnosť kódu bude meniť v závislosti od počtu prvkov na vstupe – aspoň približne. Ak sa pozrieme na hlavný cyklus v kóde:

for cislo in range(n): # n-krát
  sucet += cislo       # O(1)

Teda, výsledná rovnica je: $T(n)=1\times n=n$

🤔

Čo sa vlastne myslí pod pojmom "operácia"? Napríklad, kód vysledok = (1 + 2) * (2 ** 5) má hneď niekoľko operácií – je potrebné ich ďalej deliť?

Operácia je iba abstrakciou nad nejakou časťou kódu ktorá niečo robí. Môže ísť napríklad o vykonanie nejakej funkcie, priradenie premennej, ale aj o porovnanie a výmenu prvkov v množine (napríklad pri algoritme Bubble sort).

Operácia vyššie síce vykonáva viacero aritmetických operácií (sčítanie, umocnenie, vynásobenie), ale rátame ju iba ako jednu operáciu. Je to z toho dôvodu, že nikdy nemôžeme presne určiť časovú zložitosť algoritmu (rôzne procesory a architektúry majú rôznu rýchlosť, a tak ďalej), vnímame to na vyššej abstraktnej úrovni. Väčšinou sa jedna operácia berie ako jeden riadok kódu ktorý niečo robí.

Všeobecný postup pri výpočte časovej zložitosti

Všeobecný postup pre určenie časovej zložitosti by teda mohol vyzerať takto:

1. Identifikovať hlavnú slučku programu ktorá spracuje údaje zo vstupu, a teda jej výkon závisí od celkového množstva údajov na vstupe (zväčša od premennej $n$);
2. Zorientovať sa, čo táto časť kódu vlastne robí a koľko údajov je vlastne potrebné spracovať. Napríklad: je potrebné prejsť všetkými údajmi na vstupe, alebo môže nastať aj prípad že slučka skončí skôr? Spracujú sa všetky údaje alebo iba polovica? A podobne...;
3. Určiť časovú zložitosť operácií ktoré sú jednoznačné (deklarácia premennej, volanie funkcie, jednoduchý cyklus a podobne);
4. Prepísať to všetko ako matematické operácie a odvodiť všeobecnú funkciu pre $n$;

« Úvod do výpočtovej zložitosti

Určovanie počtu operácií v rekurzívnych volaniach »