Určovanie počtu operácií

Matematický operátor sumácie ($\sum$), aritmetická postupnosť, určovanie počtu vykonaných operácií na základe kódu v určitom programovacom jazyku.

Matematický operátor sumácie ($\sum$ – Sigma)

Keďže pre spracovanie určitého objemu údajov na vstupe (zväčša uložených v množine, poli, zozname, a podobne) sa používajú v programovacích jazykoch zväčša cykly, počet operácií sa dá vyjadriť pomocou matematického operátora sumácie – $\sum$.

Napríklad: $\sum _{i=1}^{8}1$ znamená, že $i$ začína na čísle 1 a pokračuje po 8 (vrátane). S každou iteráciou sa sčítava časť za operátorom (v tomto prípade sa teda číslo 1 sčíta presne 8 krát: $\stackrel{8}{\overbrace{1+1+1+1+1+1+1+1}}$, výsledok: $\sum _{i=1}^{8}1=8$).

Toto by sa dalo vyjadriť v kóde takto:

vysledok = 0
for i in range(8):  # vykoná sa 8 krát
    vysledok += 1
print(vysledok)  # 8

Sumácia môže mať rôzny názov a definíciu riadiacej premennej, ako aj hornú hranicu. Všetky nasledujúce zápisy sú platné:

Matematický zápis	Zápis v Python kóde
$\sum _{i=5}^{9}1$	suma = 0 for i in range(5, 10): suma += 1
$\sum _{i=0}^{n}1$	suma = 0 for i in range(n+1): suma += 1
$\sum _{j=1}^{n+1}(i+1)$	suma = 0 i = ... # napr.: môže pochádzať z vonkajšieho cyklu for j in range(1, n+2): suma += (i + 1)

Avšak, nemôžeme definovať negatívny krok. Napríklad, tento zápis nie je matematicky správny: $\sum _{j=10}^{0}1$ ($j$ by nikdy nenabudlo hodnotu 0).

Príklady pre sumáciu

Vypočítaj:

1

$\sum _{i=1}^{8}1$ =

2

$\sum _{i=1}^{5}7$ =

3

$\sum _{i=1}^{5}i$ =

Aritmetická postupnosť

Príklady vyššie sa dajú vypočítať manuálne. Ale čo ak by sme mali napríklad postupnosť 100 prvkov, napríklad: $\sum _{i=1}^{100}i$.

V tomto prípade by sa postupnosť rozbalila ako $\stackrel{?}{\overbrace{1+2+\cdots +99+100}}$. Ručne, číslo po čísle, by sme to sčítavali asi iba dlho...

Avšak, múdri matematici si všimli, že medzi číslami platí určitý vzťah. Ak zoberieme v (rozbalenej) postupnosti vždy dva protiľahlé prvky a sčítame ich, výsledkom bude vždy rovnaké číslo. To znamená, že pre výpočet súčtu všetkých členov aritmetickej postupnosti vyššie nám stačí sčítať dva protiľahlé prvky (spravidla prvý a posledný prvok), vynásobiť ich počtom prvkov a vydeliť dvomi:

Výpočet súčtu prvých 100 prvkov aritmetickej postupnosti.

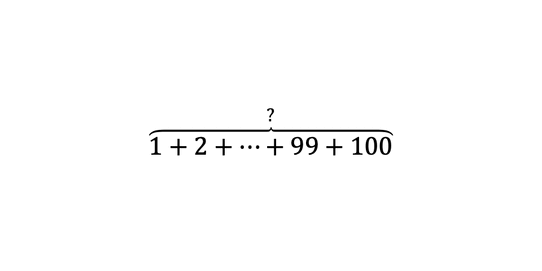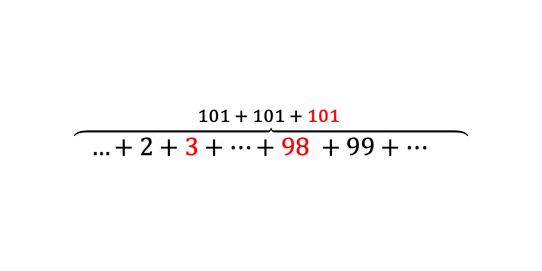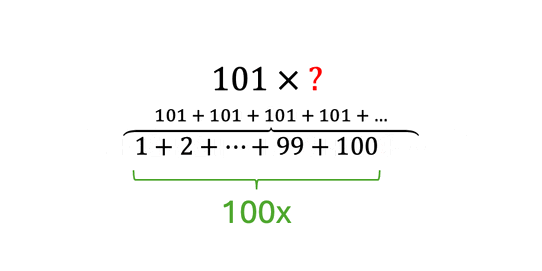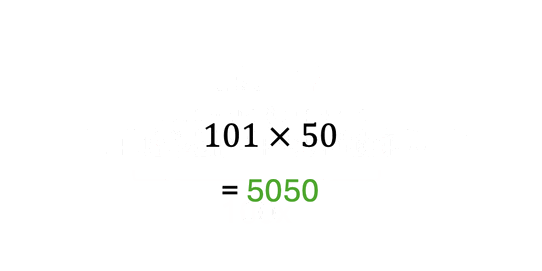
Výsledkok: $\sum _{i=1}^{100}i=50\times 101=5050$. Samozrejme, je dôležité že číselný odstup od každého prvku (respektíve, súčet dvoch protiľahlých párov) je rovnaký. Napríklad, postupnosť čísiel $1,3,5,7,11,\cdots$ nie je aritmetickou postupnosťou a teda by sme nemohli aplikovať metódu ktorá je znázornená vyššie.

Všeobecný vzorec pre výpočet súčtu $n$ prvkov aritmetickej postupnosti je:

$$\begin{array}{rl}{S}_n& =\frac{(a_1+a_n)\times n}{2}\\ \text{kde: }{a}_1& \text{ je prvý prvok (prvok na pozícií 1) }\\ a_n& \text{ je posledný prvok (na pozícií n) }\\ n& \text{ je počet prvkov }\\ \end{array}$$

Horná a dolná hranica postupnosti

Každá aritmetická postupnosť má hornú a dolnú hranicu, ktorou vyjadrujeme maximálny možný rozsah hodnôt ktoré môže postupnosť obsahovať. Spravidla:

• dolnou hranicou je prvý prvok aritmetickej postupnosti;
• hornou hranicou je posledný prvok aritmetickej postupnosti;

Počet prvkov aritmetickej postupnosti ($n$) definovanej pomocou sumácie ($\sum _{\text{i = (dolná hranica)}}^{\text{(horná hranica)}}$) môžeme vypočítať ako:

$$\text{(horná hranica)}-\text{(dolná hranica)}+1$$ (plus 1 – pretože berieme do úvahy aj prvý prvok postupnosti)

Príklady pre výpočet súčtu prvkov aritmetickej postupnosti

Vypočítaj:

1

$\sum _{i=1}^{300}i$ =

2

$\sum _{i=10}^{100}i$ =

3

$\sum _{k=24}^{365}i$ =

.

« Úvod do výpočtovej zložitosti

Určovanie počtu operácií v rekurzívnych volaniach »