More actions
Bez shrnutí editace |
Bez shrnutí editace |
||
| Riadok 1: | Riadok 1: | ||
Čo je asymptotická | Čo je asymptotická (''Big-O'') notácia, jej zmysel a interpretácia výsledkov. | ||
{{Pojmová mapa}} | {{Pojmová mapa}} | ||
| Riadok 24: | Riadok 24: | ||
# (pretože prebehne práve 1 operácia, teda vytvorenie premennej) | # (pretože prebehne práve 1 operácia, teda vytvorenie premennej) | ||
poradie_v_tyzdni = 3 | poradie_v_tyzdni = 3 # toto je stále konštanta, takže O(1) | ||
# toto je stále konštanta, takže O(1) | den = DNI[poradie_v_tyzdni-1] # znovu O(1) | ||
print(den) # O(1) | |||
den = DNI[poradie_v_tyzdni-1] | |||
# | |||
print(den) | |||
# | |||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 55: | Riadok 35: | ||
# vytvorenie premennej <code>DNI</code>; | # vytvorenie premennej <code>DNI</code>; | ||
# vytvorenie premennej <code>poradie_v_tyzdni</code>; | # vytvorenie premennej <code>poradie_v_tyzdni</code>; | ||
# | # vytvorenie premennej <code>den</code>; | ||
#výpis tejto premennej na terminál; | #výpis tejto premennej na terminál; | ||
Teda, výsledok by teoreticky mohol byť <math>O( | Teda, výsledok by teoreticky mohol byť <math>O(4)</math> (iba sčítame operácie: <math>O(1 + 1 + 1 + 1)</math>). Číslo v zátvorke by predstavovalo počet operácií ktoré kód vykoná - avšak, v praxi to nedáva zmysel, pretože cieľom nie je vypočítať presný počet operácií ktoré kód vykoná, ale iba '''určiť trend, podľa ktorého sa mení výkon algoritmu s meniacim sa objemom údajov na vstupe'''. | ||
Aby sme ale mohli správne určiť pomer výkonu k vstupu, potrebujeme pridať premennú <math>n</math>, ktorá bude udávať počet prvkov na vstupe, napríklad: | |||
<syntaxhighlight lang="python3"> | <syntaxhighlight lang="python3"> | ||
| Riadok 83: | Riadok 61: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Vidíme, že počet čísiel ktoré sa majú sčítať sa dynamicky menia v závislosti od toho čo zadá používateľ do terminálu (respektíve, podľa toho aké číslo je v premennej <math>n</math>). | |||
Z toho vyplýva, že musíme odvodiť všeobecnú rovnicu ktorá bude hovoriť, ako sa časová náročnosť kódu bude meniť v závislosti od počtu prvkov na vstupe – aspoň približne. | Z toho vyplýva, že musíme odvodiť všeobecnú rovnicu ktorá bude hovoriť, ako sa časová náročnosť kódu bude meniť v závislosti od počtu prvkov na vstupe – aspoň približne. Ak sa pozrieme na hlavný cyklus v kóde: | ||
<syntaxhighlight lang="python3"> | <syntaxhighlight lang="python3"> | ||
for cislo in range(n): # n-krát | |||
sucet += cislo # O(1) | |||
</syntaxhighlight> | </syntaxhighlight> | ||
Teda, | Teda, výsledná rovnica je: <math>O(1 \times n) = O(n)</math> (počet operácií súčtu je rovný počtu čísel ktoré máme sčítať) | ||
{{Úvaha|otazka=Čo sa vlastne myslí pod pojmom "operácia"? Aj najjednoduchšie inštrukcie môžu trvať niekoľko CPU cyklov - ako veľmi musíme kód deliť a "rozkúskovať"? A prečo nás vlastne zaujíma iba ten cyklus? Aj priradenie premennej <code>n</code> je predsa operácia?}}[[Súbor:Comparison computational complexity.svg|alt=Porovnanie výpočtovej zložitosti|žiadny|náhľad|287x287bod|Porovnanie výpočtovej zložitosti pre rôzne asymptotické správania funkcií - os Y (<math>N</math>) predstavuje (približný) počet operácií, os X (<math>n</math>) predstavuje počet prvkov na vstupe.]] | |||
''Big-O'' sa používa na vyjadrenie '''asymptotického správania algoritmu''', teda ako sa jeho výkon mení pri '''<u>veľkých</u>''' hodnotách <math>n</math>. Mohli by sme brať do úvahy aj konštantné faktory <math>O(1)</math> (napríklad, priradenie premenných mimo hlavného cyklu programu), ale nemá to zmysel pretože pri veľkom množstve vstupných hodnôt sú alokácie pár (globálnych) premenných zanedbateľné. Skúmame iba '''trend''', to znamená že ak máme napríklad dva výsledky: <math>O(1 + n)</math> a <math>O(1 000 000 + n)</math>, oba naznačujú že trend je '''lineárny''' – presný počet operácií nás nemusí zaujímať. | |||
Ak by sme mali ako výsledok napríklad <math>O(n^2 + n + 1)</math>, zredukovali by sme ho iba na <math>O(n^2)</math>, pretože táto hodnota má tendenciu rásť najrýchlejšie podľa toho ako by sa menilo <math>n</math> ('''rastie kvadraticky''', a to má prednosť pred lineárnym alebo konštantným správaním). To, že to rastie kvadraticky nám stačí a neberieme do úvahy že to ešte rastie aj lineárne a že je tam aj konštantné správanie (väčšinou by sa vo výsledku nemal nachádzať súčet, treba sa zamerať na dominantný člen). | |||
No a operácia je vlastne iba určitá abstrakcia nad nejakou časťou kódu ktorá niečo robí. Môže ísť napríklad o vykonanie nejakej funkcie, priradenie premennej, aritmetickú operáciu, atď... Ak by sme mali napríklad funkciu <code>print("ahoj")</code>, tak táto funkcia má svoju implementáciu niekde v jadre Pythonu, ale nepoznáme ju a nemôžme jednoznačne určiť jej výpočtovú zložitosť. Okrem toho sú tu jednoducho aj iné faktory (hlavným je ten, že výkon hardvéru rôznych počítačov sa líši). | |||
=== Všeobecný postup === | |||
Všeobecný postup pre určenie výpočtovej zložitosti by teda mohol vyzerať takto: | |||
# Identifikovať hlavnú slučku programu ktorá spracuje údaje zo vstupu, a teda jej výkon závisí od celkového množstva údajov na vstupe; | |||
# Zorientovať sa, čo táto časť kódu vlastne robí a koľko údajov je vlastne potrebné spracovať. Napríklad: je potrebné prejsť všetkými údajmi na vstupe, alebo môže nastať aj prípad že slučka skončí skôr? Spracujú sa všetky údaje alebo iba polovica? A podobne...; | |||
# Určiť výpočtovú zložitosť operácií ktoré sú jednoznačné; | |||
# Dať to všetko dokopy (ak je to cyklus, pravdepodobne budeme násobiť toľkokrát, koľko sa kód bude opakovať, inak sčítavame) | |||
=== Interpretácia výsledkov výpočtovej zložitosti === | |||
No, možno by bolo dobré urobiť si prehľad najčastejších výsledkov (pozri graf vyššie) a vysvetliť si ich: | No, možno by bolo dobré urobiť si prehľad najčastejších výsledkov (pozri graf vyššie) a vysvetliť si ich: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Riadok 162: | Riadok 132: | ||
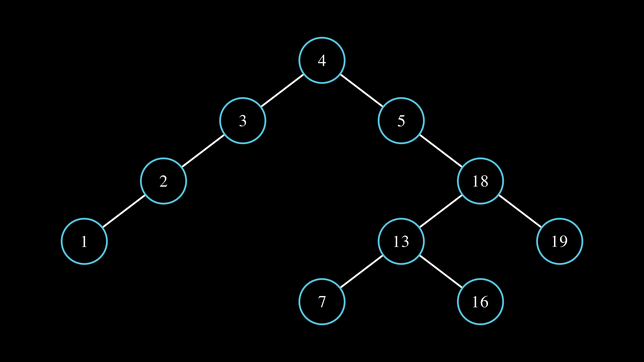
<div style="display: flex; justify-content: center;">[[Súbor:Jednoduchý binárny strom.png|alt=Jednoduchý binárny strom|644x644bod]]</div> | <div style="display: flex; justify-content: center;">[[Súbor:Jednoduchý binárny strom.png|alt=Jednoduchý binárny strom|644x644bod]]</div> | ||
Vždy je garantované, že (pri správnom aplikovaní algoritmu) vyhľadávanie nejakého prvku zaberie o polovicu menej krokov ako keby sme prehľadávali celú množinu, prvok po | Vždy je garantované, že (pri správnom aplikovaní algoritmu) vyhľadávanie nejakého prvku zaberie o polovicu menej krokov ako keby sme prehľadávali celú množinu prvok po prvku. | ||
Napríklad, povedzme že chceme nájsť číslo 13. Začíname od čísla 4 úplne hore. A zakaždým sa pýtame: je hľadané číslo (''13'') menšie alebo väčšie ako aktuálne číslo (''4'')? Ak je '''väčšie = doprava''', ak je '''menšie = doľava'''. 13 je väčšie, takže ideme doprava na číslo 5. 13 ktorú hľadáme je stále väčšia ako 5, ideme doprava na 18. 13 je menšie ako 18, ideme doľava. A práve tam končíme, pretože sme našli prvok 13 ktorí sme hľadali. | |||
Dáva to zmysel - nech je množina akákoľvek dlhá s akýmikoľvek číslami, pri vyhľadávaní budeme mať vždy iba 2 možnosti, pričom vždy môžme ísť iba po jednej vetve. Teda, '''počet vstupu ktorý musíme spracovať sa skrátil o polovicu'''. A o polovicu sa skráti aj množstvo operácií v algoritme ktoré sa musia vykonať. Matematicky sa teda skráti aj celkový čas hľadania (o polovicu), čo je vyjadrené ako <math>O(\log{n})</math>. | |||
{{Úvaha|otazka=Nemalo by to teda byť <math>O\Bigl(\frac{n}{2}\Bigr)</math>?}} | |||
Nie, je tam logaritmus. Neviem prečo. | |||
O binárnom vyhľadávaní a konkrétnej implementácií v praxi si povieme neskôr v časti o [[Binárne vyhľadávanie|binárnom vyhľadávaní]]. | O binárnom vyhľadávaní a konkrétnej implementácií v praxi si povieme neskôr v časti o [[Binárne vyhľadávanie|binárnom vyhľadávaní]]. | ||
Verzia z 18:27, 10. február 2025
Čo je asymptotická (Big-O) notácia, jej zmysel a interpretácia výsledkov.
Asymptotická notácia?
Asymptotická notácia predstavuje, koľko operácií vykoná určitý kód pre prvkov na vstupe. Inými slovami, majme napríklad tento kód pre zistenie názvu dňa podľa jeho poradia v týždni (1 až 7):
DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
# 0 1 2 3 4 5 6
poradie_v_tyzdni = 3 # tretí deň v týždni
den = DNI[poradie_v_tyzdni-1] # -1, pretože indexujeme od 0
print(den)
# "Streda"
Operácie, ktoré kód vyššie vykonáva, môžeme rozpísať a analyzovať. Interpretácia mojej analýzy je zobrazená nižšie:
DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
# alokuje sa premenná "DNI" a priradí sa jej hodnota
# z hľadiska časovej náročnosti sú konštanty O(1)
# (pretože prebehne práve 1 operácia, teda vytvorenie premennej)
poradie_v_tyzdni = 3 # toto je stále konštanta, takže O(1)
den = DNI[poradie_v_tyzdni-1] # znovu O(1)
print(den) # O(1)
Tuto sa ešte nenachádza žiadna premenná , keďže vstup sa pre kód nikdy nemení – vždy máme pevne danú množinu v ktorej je 7 prvkov (dní) a vyberáme práve jeden, nie sú tam žiadne cykly ani iné vetvenie).
Nezáleží na tom, koľkokrát kód vyššie spustíme, môžeme tvrdiť že vždy sa vykoná práve 6 operácií:
- vytvorenie premennej
DNI; - vytvorenie premennej
poradie_v_tyzdni; - vytvorenie premennej
den; - výpis tejto premennej na terminál;
Teda, výsledok by teoreticky mohol byť (iba sčítame operácie: ). Číslo v zátvorke by predstavovalo počet operácií ktoré kód vykoná - avšak, v praxi to nedáva zmysel, pretože cieľom nie je vypočítať presný počet operácií ktoré kód vykoná, ale iba určiť trend, podľa ktorého sa mení výkon algoritmu s meniacim sa objemom údajov na vstupe.
Aby sme ale mohli správne určiť pomer výkonu k vstupu, potrebujeme pridať premennú , ktorá bude udávať počet prvkov na vstupe, napríklad:
# premenná "n" môže byť akékoľvek prirodzené číslo (väčšie ako alebo rovné nule)
# deklarácia by mohla vyzerať napríklad takto:
n = int(input())
def scitaj_prvych(n):
"""
Funkcia, ktorá sčíta prvých `n` čísel a vráti výsledok sčítania.
"""
sucet = 0 # konštantné priradenie, O(1)
# toto si vysvetlíme nižšie
# (spoiler: bude nás zaujímať iba toto :))
for cislo in range(n):
sucet += cislo
return sucet # aj operácia vrátenia ("return") sa pokladá za náročnosť O(1)
Vidíme, že počet čísiel ktoré sa majú sčítať sa dynamicky menia v závislosti od toho čo zadá používateľ do terminálu (respektíve, podľa toho aké číslo je v premennej ).
Z toho vyplýva, že musíme odvodiť všeobecnú rovnicu ktorá bude hovoriť, ako sa časová náročnosť kódu bude meniť v závislosti od počtu prvkov na vstupe – aspoň približne. Ak sa pozrieme na hlavný cyklus v kóde:
for cislo in range(n): # n-krát
sucet += cislo # O(1)
Teda, výsledná rovnica je: (počet operácií súčtu je rovný počtu čísel ktoré máme sčítať)
Čo sa vlastne myslí pod pojmom "operácia"? Aj najjednoduchšie inštrukcie môžu trvať niekoľko CPU cyklov - ako veľmi musíme kód deliť a "rozkúskovať"? A prečo nás vlastne zaujíma iba ten cyklus? Aj priradenie premennej n je predsa operácia?
Big-O sa používa na vyjadrenie asymptotického správania algoritmu, teda ako sa jeho výkon mení pri veľkých hodnotách . Mohli by sme brať do úvahy aj konštantné faktory (napríklad, priradenie premenných mimo hlavného cyklu programu), ale nemá to zmysel pretože pri veľkom množstve vstupných hodnôt sú alokácie pár (globálnych) premenných zanedbateľné. Skúmame iba trend, to znamená že ak máme napríklad dva výsledky: a , oba naznačujú že trend je lineárny – presný počet operácií nás nemusí zaujímať.
Ak by sme mali ako výsledok napríklad , zredukovali by sme ho iba na , pretože táto hodnota má tendenciu rásť najrýchlejšie podľa toho ako by sa menilo (rastie kvadraticky, a to má prednosť pred lineárnym alebo konštantným správaním). To, že to rastie kvadraticky nám stačí a neberieme do úvahy že to ešte rastie aj lineárne a že je tam aj konštantné správanie (väčšinou by sa vo výsledku nemal nachádzať súčet, treba sa zamerať na dominantný člen).
No a operácia je vlastne iba určitá abstrakcia nad nejakou časťou kódu ktorá niečo robí. Môže ísť napríklad o vykonanie nejakej funkcie, priradenie premennej, aritmetickú operáciu, atď... Ak by sme mali napríklad funkciu print("ahoj"), tak táto funkcia má svoju implementáciu niekde v jadre Pythonu, ale nepoznáme ju a nemôžme jednoznačne určiť jej výpočtovú zložitosť. Okrem toho sú tu jednoducho aj iné faktory (hlavným je ten, že výkon hardvéru rôznych počítačov sa líši).
Všeobecný postup
Všeobecný postup pre určenie výpočtovej zložitosti by teda mohol vyzerať takto:
- Identifikovať hlavnú slučku programu ktorá spracuje údaje zo vstupu, a teda jej výkon závisí od celkového množstva údajov na vstupe;
- Zorientovať sa, čo táto časť kódu vlastne robí a koľko údajov je vlastne potrebné spracovať. Napríklad: je potrebné prejsť všetkými údajmi na vstupe, alebo môže nastať aj prípad že slučka skončí skôr? Spracujú sa všetky údaje alebo iba polovica? A podobne...;
- Určiť výpočtovú zložitosť operácií ktoré sú jednoznačné;
- Dať to všetko dokopy (ak je to cyklus, pravdepodobne budeme násobiť toľkokrát, koľko sa kód bude opakovať, inak sčítavame)
Interpretácia výsledkov výpočtovej zložitosti
No, možno by bolo dobré urobiť si prehľad najčastejších výsledkov (pozri graf vyššie) a vysvetliť si ich:
Najlepší prípad je konštantný faktor, teda . V analógií z reálneho života by to napríklad znamenalo, že máme balíček kariet a chceme vybrať prvú kartu – a to urobíme okamžite, bez ohľadu na to koľko kariet je v balíčku. Môže ich tam byť 32, ale mohlo by ich byť aj 1 000, no prvú kartu vyberieme vo všetkých prípadoch vždy prakticky okamžite, teda je to iba akoby sme vykonali len jednu operáciu.
Konkrétne príklady z programovania sú napríklad jednoduché aritmetické operácie (sčítanie, odčítanie, násobenie, delenie...), výber konkrétneho prvku na n-tej pozícií v indexovanom poli, vrátenie hodnoty a podobne...
Aha, máme tu aj obľúbené logaritmy! Samozrejme je za tým matematika ktorá funguje, ale pre uľahčenie života si stačí iba zapamätať:
Ak sa veľkosť spracovávaného vstupu (prvkov) skráti o polovicu, tak tento algoritmus bude mať logaritmickú rýchlosť.
Obľúbeným príkladom z praxe je napríklad binárne vyhľadávanie. Ak nevieš ako fungujú binárne stromy, tu je jeden príklad. Vľavo sú prvky ktoré sú menšie ako aktuálny rodič a vpravo sú prvky väčšie ako aktuálny rodič:
Vždy je garantované, že (pri správnom aplikovaní algoritmu) vyhľadávanie nejakého prvku zaberie o polovicu menej krokov ako keby sme prehľadávali celú množinu prvok po prvku.
Napríklad, povedzme že chceme nájsť číslo 13. Začíname od čísla 4 úplne hore. A zakaždým sa pýtame: je hľadané číslo (13) menšie alebo väčšie ako aktuálne číslo (4)? Ak je väčšie = doprava, ak je menšie = doľava. 13 je väčšie, takže ideme doprava na číslo 5. 13 ktorú hľadáme je stále väčšia ako 5, ideme doprava na 18. 13 je menšie ako 18, ideme doľava. A práve tam končíme, pretože sme našli prvok 13 ktorí sme hľadali.
Dáva to zmysel - nech je množina akákoľvek dlhá s akýmikoľvek číslami, pri vyhľadávaní budeme mať vždy iba 2 možnosti, pričom vždy môžme ísť iba po jednej vetve. Teda, počet vstupu ktorý musíme spracovať sa skrátil o polovicu. A o polovicu sa skráti aj množstvo operácií v algoritme ktoré sa musia vykonať. Matematicky sa teda skráti aj celkový čas hľadania (o polovicu), čo je vyjadrené ako .
Nemalo by to teda byť ?
Nie, je tam logaritmus. Neviem prečo.
O binárnom vyhľadávaní a konkrétnej implementácií v praxi si povieme neskôr v časti o binárnom vyhľadávaní.
.
Pravdepodobne asi najčastejší prípad v praxi. Predstavuje lineárnu rýchlosť algoritmu - inými slovami, o koľko viac prvkov pridáme do vstupu, o toľko sa spomalí algoritmus. Ak by sme mali balík kariet, znamenalo by to napríklad že chceme zrátať koľko tam tých kariet je. No a aby sme to spravili, musíme prejsť každou kartou v balíku. Ak máme 10 kariet, zrátame ich relatívne rýchlo, no pri milióne by sme už mali problém.
Poznámka: Pri výpočtovej zložitosti vždy predpokladáme že každá operácia - v našom prípade prirátanie každej karty do celkového počtu - nám zaberie rovnaký čas, napríklad pol sekundy. To znamená, že 10 kariet by sme rátali 5 sekúnd, milión kariet by sme v tom prípade rátali približne 140 hodín.
Ale ako sme hovorili predtým, zaujíma nás iba trend - pretože aj tak nedokážeme rozpočítať koľko trvajú jednotlivé procesy v počítači, napríklad koľko trvá prístup k prvku v poli (mení sa to v závislosti od výkonu hardvéru, aktuálneho zaťaženia počítača a tak ďalej...). Zaujíma nás všeobecný trend toho, ako sa výkon mení a to nám stačí pre jednoznačné určenie lepšieho algoritmu.
Najhorší prípad je . Ak si zabudol, ten "výkričník" v matematike sa nazýva faktoriál a je to súčin všetkých prvkov od po 1 – napríklad, znamená: .
znamená že máme napríklad balík kariet na ktorých sú čísla. Tieto karty chceme zoradiť od najväčšieho čísla po najmenšie. Ale robíme to takým spôsobom, že karty vyhodíme do vzduchu a dúfame že padnú na zem správne zoradené. Predpokladáme teda, že musíme vykonať všetky možné kombinácie operácií pre to, aby sme ich niekedy vytriedili správne (preto je tam ten faktoriál, kombinatorika funguje...). To môže pri malom množstve kariet trvať niekoľko minút, no pri väčších číslach sa môžeme trápiť bezvýsledne aj niekoľko rokov...
Čo je aj dôvod, prečo vlastne všetko toto počítame a analyzujeme. Je rozdiel, ak nejaký algoritmus trvá pár sekúnd versus pár rokov, že? Naším cieľom je samozrejme tvoriť algoritmy ktoré sú efektívne a prehľadné. A Big-O notácia nám umožňuje porovnávať výkon dvoch rozličných algoritmov matematicky pre veľké vstupy. A keďže sme v dobe kedy bežne pracujeme s veľkým objemom dát na dennej báze, je veľmi dôležité aby bolo všetko čo najrýchlejšie – pretože nikto nemá čas a každý sa vždy všade iba ponáhľa...