Určovanie počtu operácií

Matematický operátor sumácie ($\sum$), aritmetická postupnosť, určovanie počtu vykonaných operácií na základe kódu v určitom programovacom jazyku.

Rýchlokurz matematickej časti

Matematický operátor sumácie ($\sum$ – Sigma)

Keďže pre spracovanie určitého objemu údajov na vstupe (zväčša uložených v množine, poli, zozname, a podobne) sa používajú v programovacích jazykoch zväčša cykly, počet operácií sa dá vyjadriť pomocou matematického operátora sumácie – $\sum$.

Napríklad: $\sum _{i=1}^{8}1$ znamená, že $i$ začína na čísle 1 a pokračuje po 8 (vrátane). S každou iteráciou sa sčítava časť za operátorom (v tomto prípade sa teda číslo 1 sčíta presne 8 krát: $\stackrel{8}{\overbrace{1+1+1+1+1+1+1+1}}$, výsledok: $\sum _{i=1}^{8}1=8$).

Toto by sa dalo vyjadriť v kóde takto:

vysledok = 0
for i in range(8):  # vykoná sa 8 krát
    vysledok += 1
print(vysledok)  # 8

Sumácia môže mať rôzny názov a definíciu riadiacej premennej, ako aj hornú hranicu. Všetky nasledujúce zápisy sú platné:

Matematický zápis	Zápis v Python kóde
$\sum _{i=5}^{9}1$	suma = 0 for i in range(5, 10): suma += 1
$\sum _{i=0}^{n}1$	suma = 0 for i in range(n+1): suma += 1
$\sum _{j=1}^{n+1}(i+1)$	suma = 0 i = ... # napr.: môže pochádzať z vonkajšieho cyklu for j in range(1, n+2): suma += (i + 1)

Avšak, nemôžeme definovať negatívny krok. Napríklad, tento zápis nie je matematicky správny: $\sum _{j=10}^{0}1$ ($j$ by nikdy nenabudlo hodnotu 0).

Príklady pre sumáciu:

1

$\sum _{i=1}^{8}1$ =

2

$\sum _{i=1}^{5}7$ =

3

$\sum _{i=1}^{5}i$ =

Aritmetická postupnosť

Príklady vyššie sa dajú vypočítať manuálne. Ale čo ak by sme mali napríklad postupnosť 100 prvkov, napríklad: $\sum _{i=1}^{100}i$.

V tomto prípade by sa postupnosť rozbalila ako $\stackrel{?}{\overbrace{1+2+\cdots +99+100}}$. Ručne, číslo po čísle, by sme to sčítavali asi iba dlho...

Avšak, múdri matematici si všimli, že medzi číslami platí určitý vzťah. Ak zoberieme v (rozbalenej) postupnosti vždy dva protiľahlé prvky a sčítame ich, výsledkom bude vždy rovnaké číslo. To znamená, že pre výpočet súčtu všetkých členov aritmetickej postupnosti vyššie nám stačí sčítať dva protiľahlé prvky (spravidla prvý a posledný prvok), vynásobiť ich počtom prvkov a vydeliť dvomi:

Výpočet súčtu prvých 100 prvkov aritmetickej postupnosti.

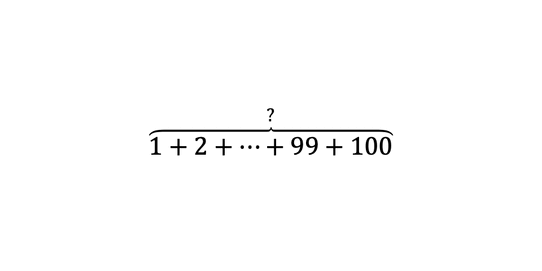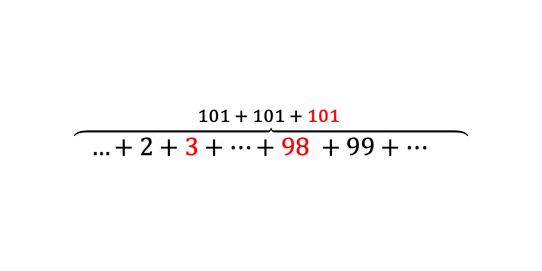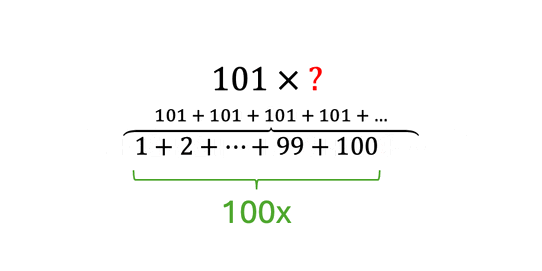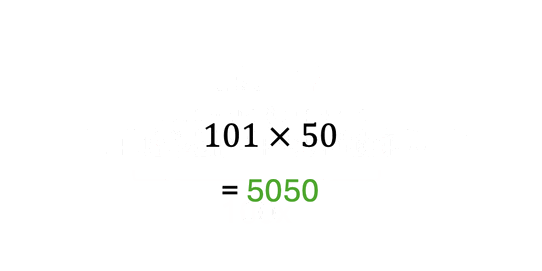
Výsledok: $\sum _{i=1}^{100}i=50\times 101=5050$. Samozrejme, je dôležité že číselný odstup od každého prvku (respektíve, súčet dvoch protiľahlých párov) je rovnaký. Napríklad, postupnosť čísiel $1,3,5,7,11,\cdots$ nie je aritmetickou postupnosťou a teda by sme nemohli aplikovať metódu ktorá je znázornená vyššie.

Všeobecný vzorec pre výpočet súčtu $n$ prvkov aritmetickej postupnosti je:

$$\begin{array}{rl}{S}_n& =\frac{(a_1+a_n)\times n}{2}\\ \text{kde: }{a}_1& \text{ je prvý prvok (prvok na pozícií 1) }\\ a_n& \text{ je posledný prvok (na pozícií n) }\\ n& \text{ je počet prvkov }\\ \end{array}$$

Horná a dolná hranica postupnosti

Každá aritmetická postupnosť má hornú a dolnú hranicu, ktorou vyjadrujeme maximálny možný rozsah hodnôt ktoré môže postupnosť obsahovať. Spravidla:

• dolnou hranicou je prvý prvok aritmetickej postupnosti;
• hornou hranicou je posledný prvok aritmetickej postupnosti;

Počet prvkov aritmetickej postupnosti ($n$) definovanej pomocou sumácie ($\sum _{\text{i = (dolná hranica)}}^{\text{(horná hranica)}}$) môžeme vypočítať ako:

$$\text{(horná hranica)}-\text{(dolná hranica)}+1$$

(plus 1 – pretože berieme do úvahy aj prvý prvok postupnosti)

Príklady pre výpočet súčtu prvkov aritmetickej postupnosti:

1

$\sum _{i=1}^{300}i$ =

2

$\sum _{i=10}^{100}i$ =

3

$\sum _{k=24}^{365}i$ =

Určovanie počtu vykonaných operácií v kóde

Poďme ale začať pekne od začiatku a krok po kroku. Začneme jednoduchými príkladmi a postupne budeme zvyšovať náročnosť.

Majme napríklad tento kód pre zistenie názvu dňa podľa jeho poradia v týždni (čiže od 1 pre pondelok až po 7 pre nedeľu):

DNI = ["Pondelok", "Utorok", "Streda", "Štvrtok", "Piatok", "Sobota", "Nedeľa"]
#           0         1          2         3         4         5          6

poradie_v_tyzdni = 3          # tretí deň v týždni
den = DNI[poradie_v_tyzdni-1] # -1, pretože indexujeme od 0

print(den)
# "Streda" – tretím dňom v týždni je streda

Tuto sa ešte nenachádza žiadna premenná $n$, keďže vstup sa pre kód nikdy nemení – vždy máme pevne danú množinu v ktorej je 7 prvkov (dní) a vyberáme práve jeden, v kóde nie sú žiadne cykly ani iné vetvy).

Nezáleží na tom, koľkokrát kód vyššie spustíme, môžeme tvrdiť že vždy sa vykonajú práve 4 operácie:

1. vytvorenie premennej DNI;
2. vytvorenie premennej poradie_v_tyzdni;
3. vytvorenie premennej den;
4. výpis tejto premennej na terminál;

Teda, $T=4$.

🤔

Čo sa vlastne myslí pod pojmom "operácia"? Napríklad, kód vysledok = (1 + 2) * (2 ** 5) má hneď niekoľko operácií – je potrebné ich ďalej deliť?

Operácia je iba abstrakciou nad nejakou časťou kódu ktorá niečo robí. Môže ísť napríklad o vykonanie nejakej funkcie, priradenie premennej, ale aj o porovnanie a výmenu prvkov v množine (napríklad pri algoritme Bubble sort).

Operácia vyššie síce vykonáva viacero aritmetických operácií (sčítanie, umocnenie, vynásobenie), ale rátame ju iba ako jednu operáciu. Je to z toho dôvodu, že nikdy nemôžeme presne určiť časovú zložitosť algoritmu (rôzne procesory a architektúry majú rôznu rýchlosť, a tak ďalej), vnímame to na vyššej abstraktnej úrovni. Väčšinou sa jedna operácia berie ako jeden riadok kódu ktorý niečo robí.

Určovanie počtu operácií v kóde pre rôzne veľkosti vstupu $n$

Aby sme dokázali vyjadriť časovú zložitosť algoritmu, musíme všeobecne vyjadriť funkciu pre zistenie počtu operácií pre dané $n$ (veľkosť vstupu) – algoritmus ktorý má menší počet operácií je efektívnejší. Funkcia, ktorá udáva počet operácií v závislosti od veľkosti vstupu je definovaná matematicky ako $T(n)$. Jej výsledná hodnota pre dané $n$ predstavuje najväčší počet operácií ktorý vykoná daný kód (pri vstupe o veľkosti $n$).

Pri týchto typoch úloh máme zadaný konkrétny kód v nejakom programovacom jazyku (napríklad v Pythone) a musíme určiť funkciu $T(n)$. Kľúčom je prepísať si kód na matematický zápis ktorý vyjadruje počet operácií a potom to čo najviac zjednodušiť a zovšeobecniť (aby sme tam mali nanajvýš iba premennú $n$, bez žiadnych riadiacich premenných ako $i$, $j$, $k$ a podobne).

Majme kód v Pythone. Chceme vyjadriť funkciu $T(n)$ pre počet výpisov:

for i in range(n):
  print("*", end="")

Už vieme, že print má konštantnú časovú zložitosť (tvárime sa, že je to jedna operácia v kóde, teda akoby číslo 1). Matematicky môžeme teda cyklus vyššie vyjadriť ako: $T(n)=\sum _{i=0}^{n-1}1$.

Využívame pritom vlastnosti funkcie range – začíname od čísla 0 a ideme až pokým nedosiahneme číslo $n$ (ktoré ale už v cykle nie je zahrnuté, pretože range vynecháva posledný prvok: range(3) => [0, 1, 2] # spolu tri prvky, ale bez 3). Dostali sme matematický zápis aritmetickej postupnosti, ktorú už vieme vyjadriť:

$T(n)=\sum _{i=0}^{n-1}1=1\times (n-1-0+1)$

Prečo: vieme, že horná hranica je $n-1$ a dolná hranica je $0$. Počet prvkov (jednotiek) teda získame ako: $\text{horná hranica}-\text{dolná hranica}+1$. Potom iba spočítame, koľkokrát sa tam nachádza číslo jedna (toľkokrát, koľko je tam prvkov, keďže všetky prvky sú 1). Teda, $1\times (n-1-0+1)$.

Po zjednodušení je konečný výsledok: $T(n)=n$. Hmm, kto by povedal že takýto kód bude volať print presne n-krát 😱? Ale aspoň sme dokázali, že naše matematické metódy fungujú...

Teraz skúsime niečo iné:

for i in range(1, 2 * n):
  print("*")
  print(".")

Úlohou je (opäť) zistiť počet volaní na funkciu print (vyjadriť to všeobecne ako matematickú funkciu časovej zložitosti – $T(n)$). Máme jeden cyklus s dvomi volaniami na print. Tento cyklus generuje čísla od 1 po 2 * n. Keďže jazyk Python nezahŕňa hornú hranicu do čísiel ktoré generuje, cyklus sa zastaví na čísle (2 * n) - 1. No a dva printy v cykle iba znamenajú, že sčítavame dve operácie (dve jednotky) – sčítavanie robíme vždy ak máme za sebou sekvenciu operácií na rovnakej úrovni odsadenia. Matematicky vieme cyklus vyššie zapísať ako:

$$\sum _{i=1}^{2n-1}(1+1)$$

Určíme počet prvkov: $\text{horná hranica}-\text{dolná hranica}+1=(2n-1)\cancel{-1}\cancel{+1}=2n-1$.

To znamená, že počet $(1+1)$ v cykle je $2n-1$. Výsledok je teda:

$$\begin{array}{rl}T(n)& =(1+1)\times (2n-1)\\ & =2\times (2n-1)\\ & =\stackrel{4n}{\overbrace{(2\times 2n)}}+\stackrel{-2}{\overbrace{(2\times \text{-1})}}\\ T(n)& =4n-2\\ \end{array}$$

ℹ️

Pri riešení týchto príkladov to kľudne preháňajme so zátvorkami, ak berieme nejakú časť s viacerými matematickými operáciami ktorá má byť chápaná ako jeden celok (napríklad, hornú alebo dolnú hranicu, alebo násobenie niečoho podľa počtu prvkov). Vtedy máme menšiu šancu že sa pomýlime keď máme napríklad tieto hodnoty neskôr násobiť v zátvorkách.

Skúsme ešte niečo ťažšie. Určme počet výpisov (volaní na print) pre nasledovný kód:

for i in range(1, n):
  print(i + n)

  for j in range(n-2):
    for k in range(n-2):
      print((i * n + j) * n + k)

    print(j * 2)

Na prvý pohľad sa to môže zdať zložité, pretože používame v printoch viacero premenných. Avšak, zaujíma nás iba počet volaní na print, nie konkrétne hodnoty ktoré sa vypíšu. Teda, nemusíme vôbec brať do úvahy čo sa v printoch nachádza.

Máme 3 cykly ktoré sú vnorené, pritom každý z nich realizuje jeden print. Keďže sekvenčné operácie sa sčítavajú a sčítavanie je kumulatívna operácia (nezáleží v akom poradí sčítavame, výsledok je rovnaký), môžeme si kód predstaviť zjednodušene. Ak k tomu ešte pridáme fakt že nás nezaujíma obsah printov, tak z hľadiska analýzy počtu operácií je tento kód identický s kódom vyššie:

for i in range(1, n):  # 1. cyklus
  print(1)
# +
  for j in range(n-2):  # 2. cyklus
    print(1)
#   +
    for k in range(n-2):  # 3. cyklus
      print(1)

To už vyzerá trochu jednoduchšie. Matematicky to môžeme zapísať ako:

$$T(n)=\stackrel{\text{1. cyklus}}{\overbrace{\sum _{i=1}^{(n)-1}}}(1+\stackrel{\text{2. cyklus}}{\overbrace{\sum _{j=0}^{(n-2)-1}}}(1+\stackrel{\text{3. cyklus}}{\overbrace{\sum _{k=0}^{(n-2)-1}}}(1)))$$

V hornej hranici nesmieme zabudnúť pridať -1, pretože Python nezahŕňa poslednú hodnotu v range (ako už vieme, cyklus skončí pri predposlednej hodnote). Ak máme viacero vnorených cyklov, začíname vždy od cyklu ktorý je najviac vnorený (pamätajme si, že počet prvkov sa vypočíta ako $\text{horná hranica}-\text{dolná hranica}+1$):

$\begin{array}{rl}\sum _{k=0}^{n-3}(1)& =1\times \stackrel{\text{počet prvkov}}{\overbrace{(n-3\cancel{-0}+1)}}\\ & =n-2\\ \end{array}$

Hodnotu z cyklu na tretej úrovni dosadíme do druhého cyklu:

$\begin{array}{rl}\sum _{k=0}^{n-3}(1+\stackrel{\text{3. cyklus}}{\overbrace{(n-2)}})& =(1+(n-2))\times \stackrel{\text{počet prvkov v 2. cykle}}{\overbrace{(n-3\cancel{-0}+1)}}\\ & =(1+n-2)\times (n-2)\\ & =(n-1)\times (n-2)\\ & =n^2-2n-n+2\\ & =n^2-3n+2\end{array}$

Nakoniec iba dopočítame vonkajší cyklus:

$\begin{array}{rl}T(n)& =\sum _{i=1}^{n-1}(1+\stackrel{\text{2. cyklus}}{\overbrace{n^2-3n+2}})\\ & =(n^2-3n+3)\times (n-1\cancel{-1+1})\\ & =n^2\times (n-1)-3n\times (n-1)+3\times (n-1)\\ & =(n^3-n^2)-(3n^2+3n)+(3n-3)\\ T(n)& =n^3-4n^2+6n-3\end{array}$

Teda, počet operácií pre kód vyššie je daný funkciou $T(n)=n^3-4n^2+6n-3$ (kde $n$ je veľkosť vstupu – číslo ≥ 1).

Správnosť zložitejších riešení môžeme overiť pre niekoľko vstupov, ak do kódu doplníme premennú ktorú budeme navyšovať pri každom volaní na print:

vstupy = range(2, 7)

for n in vstupy:
  pocet_printov = 0

  # --------------------------- #
  for i in range(1, n):
    # print(1)
    pocet_printov += 1

    for j in range(n - 2):
      # print(1)
      pocet_printov += 1

      for k in range(n - 2):
        # print(1)
        pocet_printov += 1
  # --------------------------- #

  # naša funkcia `T(n)`:
  ocakavany_pocet = (n**3) - 4*(n**2) + (6*n) - 3

  print("pre n =", n)
  print("očakávaný počet printov:", ocakavany_pocet)
  print("skutočný počet printov:", pocet_printov)
  print()

Po spustení vidíme, že očakávaný počet operácií sa zhoduje so skutočným počtom, riešenie je teda správne (pre veľkosti vstupov n od 2 po 6):

pre n = 2
očakávaný počet printov: 1
skutočný počet printov: 1

pre n = 3
očakávaný počet printov: 6
skutočný počet printov: 6

pre n = 4
očakávaný počet printov: 21
skutočný počet printov: 21

pre n = 5
očakávaný počet printov: 52
skutočný počet printov: 52

pre n = 6
očakávaný počet printov: 105
skutočný počet printov: 105

Určovanie počtu operácií v kóde pre rôzne veľkosti vstupu $n$ (s riadiacimi premennými)

Častokrát sa stane, že počas cyklu používame aj riadiacu premennú (napríklad $i$) ktorá mení svoju hodnotu s každou iteráciou. Túto premennú použijeme pre definovanie cyklu, ktorý má za hornú alebo dolnú hranicu túto premennú. Určenie funkcie $T(n)$ môže byť pre takéto cykly zložité, pretože nemôžme jednoznačne určiť akú hodnotu bude mať $i$ s každou iteráciou v cykle.

Majme napríklad cyklus $\sum _{i=1}^{n}i$. Všeobecne je to jednoducho $n\times i$, avšak my odtiaľ potrebujeme nejako dať preč premennú $i$. Veci sa môžu veľmi rýchlo skomplikovať a pre začiatočníkov môže byť analýza takýchto cyklov náročná.

Keď nevieme ako sa pohnúť ďalej, tak je dobrý nápad si cyklus rozpísať s konkrétnymi číslami namiesto $i$ (objaví sa nám vzor, podľa ktorého dokážeme identifikovať vzťahy medzi jednotlivými iteráciami a odvodiť všeobecný vzorec). Teda, cyklus vyššie je v podstate:

$$\sum _{i=1}^{n}i=1+2+3+\cdots +(n-1)+n$$

Prvým prvkom je vždy číslo 1 (pretože tak je to definované pod sumou: $i=1$) a posledným prvkom je $n$ (čo vidíme hore). Počet prvkov vieme zistiť pomocou vzorca: $\text{(horná hranica)}-\text{(dolná hranica)}+1=n-1+1=n\text{ prvkov}$ (je to očividné, avšak môže to pomôcť v prípade ak cyklus začína od čísla iného ako 1, aby sme sa zbytočne nepomýlili).

Ak máme tieto informácie, vieme ich vložiť do vzorca pre výpočet súčtu $n$ prvkov aritmetickej postupnosti. Vtedy získame funkciu $T(n)$:

$$\begin{array}{rl}{S}_n& =\frac{(a_1+a_n)\times n}{2}\\ T(n)& =\frac{(1+n)\times n}{2}\\ & =\frac{(n^2+n)}{2}\\ \end{array}$$

Výsledok: počet operácií pre ľubovoľnú veľkosť vstupu $n$ môžeme určiť ako $T(n)=\frac{(n^2+n)}{2}$.

Pri takomto type úloh sa treba zamyslieť že medzi prvým a posledným prvkom môže byť akákoľvek veľká postupnosť čísiel – preto rozpíšeme iba zopár, aby sme videli vzory ktoré sa opakujú a vedeli pre ne lepšie odvodiť všeobecnú funkciu. Zameriavame sa na to, o aký typ postupnosti sa jedná (aritmetická/geometrická – o tej bude reč v ďalšej téme), ktorý prvok je prvý a ktorý posledný a koľko je dokopy všetkých prvkov.

Presuňme sa na analýzu konkrétnych zdrojových kódov v praxi. Majme napríklad:

n = int(input("n: "))
op = 0

for i in range(n):
  for j in range(i):
    op += 1

print(op)

Cieľom je určiť, koľkokrát sa vykoná súčet (respektíve, koľkokrát sa vykoná riadok číslo 6) pre nejakú veľkosť vstupu $n$.

Prepíšeme cyklus (riadok 4 až 6) na matematický zápis (nesmieme zabudnúť od každej hornej hranice odpočítať 1, keďže sa jedná o Python cykly a konečná hodnota sa v cykle nevyskytuje):

$$T(n)=\sum _{i=0}^{n-1}\left(\sum _{j=0}^{i-1}1\right)$$

Vyjadrime vnútorný cyklus. Otázka je, koľko je tam jednotiek. Alebo inými slovami, koľko prvkov obsahuje cyklus? Získame to pomocou známeho vzorca: $\text{horná hranica}-\text{dolná hranica}+1$. Teda:

$$\sum _{j=0}^{i-1}1=i-1\cancel{-0}+1=i$$

Vypadá to, že vnútorný cyklus sa vykoná $i$-krát. Samozrejme že áno – veď predsa tak je definovaný cyklus! To znamená, že niekedy sa stačí pozrieť iba na kód a hneď vieme vydedukovať koľko tam bude operácií. Toto ale ešte nie je koniec, pretože prichádza na rad vonkajší cyklus. Dosaďme doň namiesto vnoreného cyklu už vypočítané $i$:

$$T(n)=\sum _{i=0}^{n-1}i$$

Tuto začína byť (už vyššie spomínaný) problém. Vieme zistiť, že tam bude $n\times i$ – ale to predsa nemôžeme použiť, pretože $i$ sa s každou iteráciou zvyšuje o 1! Počkať, ale veď toto vlastne spĺňa vlastnosti aritmetickej postupnosti. Cyklus vyzerá nejako takto:

$$\begin{array}{rl}T(n)& =\sum _{i=0}^{n-1}i\\ & =0+1+2+\cdots +(n-2)+(n-1)\\ \end{array}$$

Dospeli sme k zisteniu, že bez ohľadu na to akú hodnotu bude mať $i$, tak vždy bude prvý prvok $0$ a posledný $n-1$. Počet prvkov (opakovaní) je $n$. Krok medzi prvkami je vždy rovnaký, pretože premenná $i$ sa s každou iteráciou navyšuje o rovnaké číslo = 1. Tieto informácie nám dovolia dosadiť hodnoty do vzora pre súčet prvkov aritmetickej postupnosti a vyjadriť funkciu $T(n)$:

$$\begin{array}{rl}T(n)& =\frac{(\cancel{0}+n-1)\times n}{2}\\ & =\frac{(n^2-n)}{2}\end{array}$$

Výsledok je teda: $T(n)=\frac{(n^2-n)}{2}$.

Teraz je čas na niečo ešte ťažšie. Čo ak bude krok negatívny?

for i in range(n, 0, -1):
  for j in range(i, n + 1):
      print('*', end='')
  print()

V tomto prípade nás zaujíma, koľkokrát sa vykoná print: musíme opäť vyjadriť $T(n)$. Je tu ale problém – sumácia v matematike typicky používa kladný krok, nie záporný. Pre vonkajší cyklus teda nemôžme použiť tento zápis: $\sum _{i=n}^1$, musíme si range(n, 0, -1) otočiť – prvý argument vnímať ako hornú hranicu a druhý ako dolnú. Bude to fungovať, ale musíme si dať pozor aby sme generovali rovnaké čísla. Všeobecný postup je:

1. Vybrať z range(x, y, -1) prvé číslo x ako hornú hranicu. Od tejto hranice sa 1 nebude odpočítavať;
2. Vybrať druhé číslo y ako dolnú hranicu a pripočítať 1;

Cieľom je, aby sme range iba zrkadlovo otočili:

n = 5
cisla = range(n, 0, -1)
# (5, 4, 3, 2, 1)

zrkadlove_cisla = range(1, n+1) # v matematickom zápise túto +1 opäť odčítame
# (1, 2, 3, 4, 5)

Matematicky môžeme teda pôvodný kód zapísať ako:

for i in range(n, 0, -1):
  for j in range(i, n + 1):
      print('*', end='')
  print()

$$T(n)=\stackrel{\text{vonkajší cyklus}}{\overbrace{\sum _{i=0+1}^{n\cancel{+1-1}}(\underset{\text{vnútorný cyklus}}{\underbrace{\sum _{j=i}^{n\cancel{+1-1}}(1)}}+1)}}$$

Pre vnútorný cyklus zistíme počet jednotiek (operácií) ktoré sa sčítajú:

$$\sum _{j=i}^n(1)=1\times (n-i+1)=n-i+1$$

Dosadíme do vonkajšieho cyklu. Cyklus rozpíšeme – namiesto $i$ postupne zakaždým navyšujeme číslo o 1. Výsledkom je zložitejšia postupnosť:

$$\begin{array}{rl}T(n)& =\sum _{i=1}^n\left(n-i+1+1\right)\\ & =\sum _{i=1}^n\left(n-i+2\right)\\ & =(\stackrel{i=1}{\overbrace{n-1+2}})+(\stackrel{i=2}{\overbrace{n-2+2}})+(\stackrel{i=3}{\overbrace{n-3+2}})+(\stackrel{i=4}{\overbrace{n-4+2}})+\cdots +(\stackrel{i=n}{\overbrace{\cancel{n-n}+2)}}\\ \end{array}$$

V tejto postupnosti nás ale zaujíma iba prvý a posledný prvok (aritmetická postupnosť). Vo výpočte aritmetickej postupnosti pokračujeme takto:

$$\begin{array}{rl}T(n)& =\stackrel{a_1}{\overbrace{(n-1+2)}}+\cdots +\stackrel{a_n}{\overbrace{2}}\\ & =\stackrel{\text{počet prvkov je}n}{\overbrace{(n+1)+\cdots +2}}\\ S(n)=\frac{(a_1+a_n)\times n}{2}& =\frac{(n+1+2)\times n}{2}=\\ & =\frac{(n+3)\times n}{2}\\ T(n)& =\frac{n^2+3n}{2}\\ \end{array}$$

Poďme na ďalší kód:

for i in range(1, n + 1):
    for j in range(n - 1, i - 1, -1):
        print(" ", end="")
    for j in range(1, 2 * i):
        print("*", end="")
    print()

Máme jeden vonkajší a dva vnútorné cykly. Ako vždy, prvým krokom je prepísať kód na matematický zápis:

$$T(n)=\sum _{i=1}^{n\cancel{+1-1}}(\sum _{j=i}^{n-1}(1)+\sum _{j=1}^{2i-1}(1)+1)$$

V zápise vyššie sú už vyjadrené všetky cykly a printy. Cieľom je výraz zjednodušiť a zistiť, koľkokrát sa volá print pre nejaké $n$. V druhom cykle zľava sme zrkadlovo otočili range (teda, k druhému argumentu i - 1 sme pripočítali 1 a použili ako dolnú hranicu a n - 1 bude horná hranica).

Začíname od vnútorných cyklov:

$$\begin{array}{rl}T(n)& =\sum _{i=1}^{n\cancel{+1-1}}(\stackrel{\text{horná hranica}-\text{dolná}+1}{\overbrace{(n-1-i+1)}}+\sum _{j=1}^{2i-1}(1)+1)\\ & =\sum _{i=1}^n((n\cancel{-1}-i\cancel{+1})+(2i-1\cancel{-1}\cancel{+1})+1)\\ & =\sum _{i=1}^n((n-i)+(2i-1)+1)\\ T(n)& =\sum _{i=1}^n(n+i)\\ \end{array}$$

Zostal nám iba vonkajší cyklus. Máme tam $i$, tak ho rozpíšeme:

$\begin{array}{rl}T(n)& =\stackrel{\text{počet prvkov:}n}{\overbrace{\sum _{i=1}^n(n+\text{i})}}\\ & =\stackrel{i=1}{\overbrace{(n+1)}}+\stackrel{i=2}{\overbrace{(n+2)}}+\stackrel{i=3}{\overbrace{(n+3)}}+\cdots +\stackrel{i=(n-2)}{\overbrace{(n+(n-2))}}+\stackrel{i=(n-1)}{\overbrace{(n+(n-1))}}+\stackrel{i=n}{\overbrace{(n+n)}}\\ & =\stackrel{a_1}{\overbrace{(n+1)}}+\cdots +\stackrel{a_n}{\overbrace{(2n)}}\\ & =\frac{((n+1)+2n)\times n}{2}\\ & =\frac{(3n+1)\times n}{2}\\ T(n)& =\frac{3n^2+n}{2}\\ \end{array}$

Skúsme komplexnejší kód:

for i in range(n):
  print("*")
  print("*")

for i in range(1, n - 1):
  print("*")
  print("*")

for i in range(1, n - 1):
  for j in range(1, i + 1):
    print("*")

Prvý cyklus sa vykoná $n$ krát, vnútri cyklu sú dve operácie. Hneď to môžeme vyjadriť ako $2n$.

Dole sú ďalšie dva cykly. Druhý cyklus:

$$\sum _{i=1}^{(n-1-1)}2=2\times (n-2\cancel{-1+1})=2n-4$$

Tretí cyklus:

$$\begin{array}{rl}& \sum _{i=1}^{(n-1-1)}\left(\sum _{j=1}^{i\cancel{+1-1}}1\right)=\\ =& \sum _{i=1}^{(n-2)}(i-1+1)=\\ =& \sum _{i=1}^{(n-2)}\left(i\right)=1+2+3+\cdots +(n-2)\\ =& \frac{(1+(n-2))\times \stackrel{\text{horná hranica - dolná + 1}}{\overbrace{(n-2\cancel{-1+1})}}}{2}\\ =& \frac{(n-1)\times (n-2)}{2}\\ =& \frac{n^2-2n-n+2}{2}\\ =& \frac{n^2-3n+2}{2}\\ \end{array}$$

Nakoniec musíme iba všetky 3 cykly sčítať a dostaneme funkciu $T(n)$:

$$\begin{array}{rl}T(n)& =(2n)+(2n-4)+\frac{n^2-3n+2}{2}\\ & =4n-4+\frac{n^2-3n+2}{2}\\ & =\frac{8n-8+n^2-3n+2}{2}\\ T(n)& =\frac{n^2+5n-6}{2}\\ \end{array}$$

« Úvod do výpočtovej zložitosti

Určovanie počtu operácií v rekurzívnych volaniach »