More actions
Bez shrnutí editace |
Bez shrnutí editace |
||
| (35 medziľahlých úprav od rovnakého používateľa nie je zobrazených.) | |||
| Riadok 1: | Riadok 1: | ||
Triediace algoritmy [[Triediace algoritmy a ich výpočtová zložitosť#Bubble-sort|Bubble-sort]], [[Triediace algoritmy a ich výpočtová zložitosť# | Triediace algoritmy [[Triediace algoritmy a ich výpočtová zložitosť#Bubble-sort|Bubble-sort]], [[Triediace algoritmy a ich výpočtová zložitosť#Selection-sort|Selection-sort]], [[Triediace algoritmy a ich výpočtová zložitosť#Insertion-sort|Insertion-sort]], [[Triediace algoritmy a ich výpočtová zložitosť#Quick-sort|Quick-sort]], [[Triediace algoritmy a ich výpočtová zložitosť#Radix-sort|Radix-sort]], [[Triediace algoritmy a ich výpočtová zložitosť#Counting-sort|Counting-sort]], [[Triediace algoritmy a ich výpočtová zložitosť#Heap-sort|Heap-sort]], [[Triediace algoritmy a ich výpočtová zložitosť#Merge-sort|Merge-sort]], pojmy [[Triediace algoritmy a ich výpočtová zložitosť#Inverzia|inverzia]], [[Triediace algoritmy a ich výpočtová zložitosť#Stabilita triediaceho algoritmu|stabilný (triediaci) algoritmus]] a [[Triediace algoritmy a ich výpočtová zložitosť#Heap (halda)|heap (halda)]]. | ||
{{Pojmová mapa}} | {{Pojmová mapa}} | ||
| Riadok 6: | Riadok 6: | ||
Častým problémom v algoritmizácií je efektívne (rýchle a pamäťovo nenáročné) triedenie množiny údajov, hľadanie najväčšieho a najmenšieho čísla (respektíve, maximálnej a minimálnej hodnoty), hľadanie mediánu (prostrednej hodnoty) a modusu (hodnoty s najčastejším výskytom) a podobne. | Častým problémom v algoritmizácií je efektívne (rýchle a pamäťovo nenáročné) triedenie množiny údajov, hľadanie najväčšieho a najmenšieho čísla (respektíve, maximálnej a minimálnej hodnoty), hľadanie mediánu (prostrednej hodnoty) a modusu (hodnoty s najčastejším výskytom) a podobne. | ||
Majme napríklad množinu čísiel: <math>\{ 5,\ 2,\ 10,\ 1,\ -6 \}</math>. Ako naprogramovať algoritmus ktorý takúto množinu usporiada od najmenšieho čísla po najväčšie? Touto otázkou sa zaoberali už tvorcovia algoritmov pred nami, a v súčasnosti existuje hneď niekoľko algoritmov. Každý algoritmus má svoju výpočtovú zložitosť – niektoré sú efektívnejšie pri menšom počte vstupných hodnôt, iné sú zamerané pre triedenie veľkého množstva hodnôt. Neexistuje teda definitívna odpoveď | Majme napríklad množinu čísiel: <math>\{ 5,\ 2,\ 10,\ 1,\ {\text{-}6} \}</math>. Ako naprogramovať algoritmus ktorý takúto množinu usporiada od najmenšieho čísla po najväčšie? Touto otázkou sa zaoberali už tvorcovia algoritmov pred nami, a v súčasnosti existuje hneď niekoľko algoritmov. Každý algoritmus má svoju výpočtovú zložitosť – niektoré sú efektívnejšie pri menšom počte vstupných hodnôt, iné sú zamerané pre triedenie veľkého množstva hodnôt. Neexistuje teda definitívna odpoveď na to, ktorý algoritmus je najlepší (ale samozrejme vo všeobecnosti vždy hľadáme algoritmus s najmenšou zložitosťou, či už časovou alebo pamäťovou). | ||
V príklade vyššie sú uvedené čísla, ale samozrejme triedenie môžeme realizovať nad všetkým | V príklade vyššie sú uvedené čísla, ale samozrejme triedenie môžeme realizovať nad všetkým, čomu rozumieme že má nejakú postupnosť (napríklad: abecedný zoznam, zoradiť veľkosti objektov od najväčšieho po najmenší, usporiadanie farebného spektra, triedenie dátumov, postupnosť dní v týždni, knižné kapitoly a podobne). Neexistuje algoritmus ktorý dokáže realizovať triedenie súčasne na všetkých možných množinách prvkov (napríklad, usporiadanie písmen na klávesnici je iné ako abecedná postupnosť tých istých písmen), preto tieto algoritmy väčšinou prispôsobujeme našim potrebám. | ||
=== Bubble-sort === | === Bubble-sort === | ||
| Riadok 17: | Riadok 17: | ||
V príklade vyššie je na vstupe pole s 5 číslami. Algoritmus bubble sort obsahuje dva vnorené cykly: | V príklade vyššie je na vstupe pole s 5 číslami. Algoritmus bubble sort obsahuje dva vnorené cykly: | ||
# '''Vonkajší cyklus''' zabezpečuje prechod od posledného indexu poľa k prvému. Je to preto, že s každou iteráciou v tomto cykle je garantované, že sa usporiada práve jedno číslo ("vybublá", preto sa tento algoritmus nazýva bubble-sort). Je zbytočné kontrolovať čísla, ktoré už boli správne vytriedené | # '''Vonkajší cyklus''' zabezpečuje prechod od posledného indexu poľa k prvému. Je to preto, že s každou iteráciou v tomto cykle je garantované, že sa usporiada práve jedno číslo ("vybublá", preto sa tento algoritmus nazýva bubble-sort). Je zbytočné kontrolovať čísla, ktoré už boli správne vytriedené – preto tento cyklus začína od konca a <code>i</code> sa s každou iteráciou znižuje. | ||
# '''Vonkajší cyklus''' je ten, ktorý realizuje triedenie (porovnávanie dvoch susedných prvkov). Ak je prvý prvok väčší ako prvok ktorý nasleduje, tak sa vymenia. S každou iteráciou sa najväčšie prvky budú posúvať doprava, takže pole bude zoradené od najmenšieho po najväčší (vzostupne). Ak je potrebné čísla zoradiť naopak (od najväčšieho po najmenší, teda zostupne), tak stačí obrátiť znak porovnania (zmeniť podmienku na <code>if pole[j] < pole[j + 1]</code>). | # '''Vonkajší cyklus''' je ten, ktorý realizuje triedenie (porovnávanie dvoch susedných prvkov). Ak je prvý prvok väčší ako prvok ktorý nasleduje, tak sa vymenia. S každou iteráciou sa najväčšie prvky budú posúvať doprava, takže pole bude zoradené od najmenšieho po najväčší (vzostupne). Ak je potrebné čísla zoradiť naopak (od najväčšieho po najmenší, teda zostupne), tak stačí obrátiť znak porovnania (zmeniť podmienku na <code>if pole[j] < pole[j + 1]</code>). | ||
Je to v podstate algoritmus, ktorý posúva maximálne prvky doprava (alebo doľava, ak triedime zostupne), čím sa prvky zotriedia ("vybublajú") na správne miesto. | Je to v podstate algoritmus, ktorý posúva maximálne prvky doprava (alebo doľava, ak triedime zostupne), čím sa prvky zotriedia ("vybublajú") na správne miesto. | ||
Algoritmus bubble-sort má časovú výpočtovú zložitosť <math>O(n^2)</math>, '''je to jeden z najmenej efektívnych algoritmov'''. Používame ho napríklad vtedy, keď: | Algoritmus bubble-sort má časovú výpočtovú zložitosť <math>O(n^2)</math> (v najhoršom prípade), '''je to jeden z najmenej efektívnych algoritmov'''. Používame ho napríklad vtedy, keď: | ||
* Triedime menší počet hodnôt a teda takáto výpočtová zložitosť je pre nás akceptovateľná; | * Triedime menší počet hodnôt a teda takáto výpočtová zložitosť je pre nás akceptovateľná; | ||
| Riadok 31: | Riadok 31: | ||
<iframe frameborder="0" style="width: 100%" height="645" src="https://coding.poznamkovac.eu/?lang=sk#/embed/python/algoritmy/triedenie/1"></iframe> | <iframe frameborder="0" style="width: 100%" height="645" src="https://coding.poznamkovac.eu/?lang=sk#/embed/python/algoritmy/triedenie/1"></iframe> | ||
=== | ==== Inverzia ==== | ||
Inverzia je '''dvojica prvkov, ktoré majú zlé poradie''' (v závislosti od toho, ako by sme chceli aby boli prvky usporiadané). | |||
Napríklad, ak máme množinu čísiel <math>\{ 1, {\color{goldenrod}3}, {\color{goldenrod}2}, 4, 5 \}</math> ktorá má byť zoradená od najmenšieho čísla po najväčšie, tak dvojica prvkov <math>\{ 3, 2 \}</math> má zlé poradie. Teda, môžeme povedať že táto množina má 1 inverziu. Ak by malo byť pole zoradené od najväčšieho čísla po najmenšie, tak toto pole má hneď 9 inverzií (aby bolo pole usporiadané, tak by sme museli spraviť 9 výmien). | |||
Existuje algoritmus, podľa ktorého dokážeme zistiť počet inverzií. Pre pole vyššie by sme postupovali takto (pokiaľ by pole malo byť usporiadané '''od najväčšieho po najmenší'''): | |||
# Vyberieme si stranu z ktorej začneme – buď od ľavej strany alebo od pravej. Povedzme, že si vyberieme ľavú. '''Prvým prvkom v poli zľava je číslo <math>1</math>'''. | |||
# Spočítame, '''ktoré prvky na pravej strane od 1 sú väčšie ako 1'''. Sú to '''štyri''' čísla: <math>\{ 3, 2, 4, 5 \}</math>. | |||
# Ak sme vyčerpali všetky čísla, presunieme sa o jedno miesto doľava a zopakujeme postup. Od čísla 3 sú napravo väčšie dve čísla: <math>\{ 4, 5 \}</math>. Od čísla 2 sú to opäť tie isté dve čísla. Od 4 je väčšie jedno číslo (<math>5</math>). | |||
# Nakoniec iba spočítame všetky väčšie čísla napravo od každého čísla (to, čo sme teraz zisťovali). Teda: '''<math>4 + 2 + 2 + 1 = 9</math> inverzií'''. | |||
Ak by sme mali usporiadať pole opačne (od najmenšieho po najväčší), postupovali by sme rovnako – iba s tým rozdielom, že by sme hľadali '''prvky ktoré sú na pravej strane menšie''' ako aktuálne číslo. | |||
Inverzie sa vyskytujú vo všetkých štruktúrach ktoré nie sú správne zoradené a od ktorých očakávame nejaké poradie. Môže to byť napríklad abecedný zoznam mien, zoznam objektov ktoré majú byť zoradené podľa veľkosti ale aj postupnosť dní v týždni – všetko, čo má nejaké poradie. | |||
{{Box | |||
| text = <i>Poznámka:</i> predpokladáme, že <b>pri odstraňovaní inverzií smieme meniť iba dva susedné prvky</b> (presne ako v bubble-sorte).<br/> | |||
Počet inverzií môžeme zistiť pomocou algoritmu v bubble-sorte tak, že vytvoríme na začiatku premennú ktorá predstavuje počet inverzií (na začiatku má hodnotu <code>0</code>), a toto počítadlo zvýšime vždy o 1 keď v bubble-sorte vymeníme dva susedné prvky. Po ukončení vonkajšieho cyklu bude táto premenná obsahovať počet inverzií pre dané pole. | |||
| emoji = ℹ️ | |||
}} | |||
===== Úlohy pre určenie počtu inverzií ===== | |||
<quiz display="simple"> | |||
{ Urči počet inverzií v nasledujúcich množinách čísiel, ktoré majú byť zoradené '''vzostupne''' (od najmenšieho po najväčší (odpovede píš číslom, napríklad: <code>1</code>) | |||
|type="{}"} | |||
<math>\{ 1, 3, 2 \}</math>, počet inverzií: { 1 _2 }. | |||
<math>\{ 12, 5, 8, 0, 4 \}</math>, počet inverzií: { 8 _2 }. | |||
<math>\{ 1, 2, 3, 4, 5 \}</math>, počet inverzií: { 0 _2 }. | |||
{ Koľko inverzií je v nasledujúcom zozname dní v týždni, ak chceme aby boli dni zoradené správne podľa poradia (od Pondelka po Nedeľu)? | |||
|type="{}"} | |||
Pondelok, Streda, Utorok, Piatok, Nedeľa, Štvrtok, Sobota | |||
Počet inverzií: { 4 _2 } | |||
</quiz> | |||
=== Selection-sort === | |||
Selection-sort (''triedenie výberom'') algoritmus vyberá z poľa prvkov najmenší prvok a presunie ho na začiatok. | |||
[[Súbor:Select sort.mp4|stred|448x448bod|bezrámu]] | [[Súbor:Select sort.mp4|stred|448x448bod|bezrámu]] | ||
. | Výpočtová zložitosť tohto algoritmu je <math>O(n^2)</math>. Vo všeobecnosti je rýchlejší ako [[Triediace algoritmy a ich výpočtová zložitosť#Bubble-sort|bubble-sort]], avšak pomalší ako insertion-sort. | ||
=== Insertion-sort === | |||
Insertion-sort (''triedenie priamym vkladaním'') používa jednu časť triedeného poľa pre ukladanie už vytriedených hodnôt a druhú časť toho istého poľa pre hodnoty ktoré ešte nemajú správne poradie. Princíp je podobný ako pri [[Triediace algoritmy a ich výpočtová zložitosť#Selection-sort|selection-sorte]]. | |||
Časová výpočtová zložitosť je <math>O(n^2)</math>. Avšak narozdiel od [[Triediace algoritmy a ich výpočtová zložitosť#Selection-sort|selection-sortu]], rýchlosť insertion-sortu závisí od vstupného poľa – pre takmer utriedené pole prebehne veľmi rýchlo. | |||
=== Quick-sort === | |||
Ako už napovedá názov, quick-sort je jeden z najrýchlejších triediacich algoritmov. Quick-sort funguje vo všeobecnosti takto: | |||
# Z poľa hodnôt sa vyberie jeden prvok ako pivot; | |||
# Zvyšok poľa sa zoradí tak, že hodnoty menšie ako pivot budú naľavo od neho a hodnoty väčšie ako pivot budú napravo; | |||
# Pivot sa vymení s prvým prvkom v podmnožine s väčšími hodnotami tak, aby pivot spadol medzi menšie a väčšie hodnoty – to rozdelí pôvodné pole na dve podmnožiny, kde menšie prvky sú naľavo a väčšie napravo; | |||
# Celý postup sa rekurzívne opakuje pre obe podmnožiny menších prvkov naľavo a väčších prvkov napravo. Ak nezostane žiadna podmnožina pre ďalšie triedenie, pole je zoradené a rekurzia sa ukončí (triviálny prípad). | |||
Implementácia quick-sortu je komplexnejšia, preto pripájam už hotový algoritmus v Pythone: | |||
<iframe frameborder="0" style="width: 100%" height="645" src="https://coding.poznamkovac.eu/?lang=sk#/embed/python/algoritmy/triedenie/2"></iframe>Časová výpočtová zložitosť algoritmu quick-sort je v najhoršom prípade <math>O(n \times log_2 n)</math>, avšak v priemernom prípade je to iba <math>\Theta(n \times log_2 n)</math>, preto je v priemere oveľa efektívnejší ako ostatné algoritmy a patrí medzi najrýchlejšie triediace algoritmy. | |||
=== Radix-sort === | |||
Radix-sort je triediaci algoritmus, ktorý triedi väčšie číselné hodnoty na základe ich cifier, začína od najmenej významnej číslice (sprava doľava). Radix predstavuje základ čísla – v našej (desiatkovej) číselnej sústave máme 10 číslic: od 0 po 9. | |||
Výpočtová zložitosť tohto algoritmu sa dá všeobecne uviesť ako <math>O(n \times k)</math>, kde <math>n</math> je počet hodnôt ktoré sa majú vytriediť a <math>k</math> predstavuje počet cifier v najväčšej hodnote (z <math>n</math>). Najlepším prípadom je ten, keď má tento algoritmus veľa hodnôt pre triedenie ale všetky hodnoty majú nízky počet číslic (napríklad, triedenie 1 milióna hodnôt ktoré majú rozsah 0 – 999, teda maximálne 3 cifry). V takýchto prípadoch sa časová výpočtová zložitosť môže zjednodušiť iba ako <math>O(n)</math>. | |||
Radix-sort je algoritmus, ktorý by pre správne fungovanie mal byť naprogramovaný ako '''stabilný'''. | |||
==== Stabilita triediaceho algoritmu ==== | |||
Algoritmus triedenia sa považuje za stabilný, '''ak sa po zoradení zachová relatívne poradie rovnakých prvkov'''. Nestabilný algoritmus zachovanie tohto poradia negarantuje. | |||
Povedzme napríklad, že máme zoznam písmen abecedy ktoré obsahujú určitú hodnotu (môže to byť napríklad počet ľudí ktorí považujú toto písmeno za ich obľúbené). Chceme tento zoznam zoradiť od najobľúbenejšieho písmena po najmenej obľúbené. Ak majú dve susedné písmená rovnakú obľúbenosť, zoradíme ich podľa ich abecedného poradia. | |||
Majme napríklad písmená "'''K'''" a "'''L'''", pričom '''obidve majú hodnotu 240'''. Stabilný algoritmus správne zoradí písmená ako "K" a za ním bude nasledovať "L", avšak nestabilný algoritmus (ktorý triedi iba na základe obľúbenosti a neberie ohľad na abecednú postupnosť) by ich mohol zoradiť ako "L" a "K", čo je avšak nesprávne pretože nie je zachovaná relatívna postupnosť prvkov (na základe obľúbenosti ako primárneho zoradenia) a takýto algoritmus je '''nestabilný'''. | |||
=== Counting-sort === | |||
Tento algoritmus usporiada prvky v množine tak, že spočíta koľkokrát sa tam daný prvok nachádza. Je to užitočné, ak máme veľa opakujúcich sa hodnôt a malú rôznorodosť dát. V najhoršom prípade má výpočtovú zložitosť <math>O(n^2)</math>. | |||
=== Heap-sort === | |||
Heap-sort (haldové triedenie) je triediaci algoritmus, ktorý využíva heap (haldu) pre efektívne triedenie prvkov. Je vnímaný ako optimalizácia [[Triediace algoritmy a ich výpočtová zložitosť#Selection-sort|selection-sortu]], pretože heap nám umožní rýchlo nájsť v poli minimálnu (alebo maximálnu) hodnotu pre zámenu v <math>O(log_2 n)</math> čase namiesto <math>O(n)</math>. V dôsledku toho má tento algoritmus celkovú výpočtovú zložitosť <math>O(n \times log_2 n)</math>. | |||
==== Heap (halda) ==== | |||
Heap (halda) je dátová štruktúra, ktorá spĺňa vlastnosti heapu (haldy). Je vhodná pre prípady keď potrebujeme častokrát uchovávať maximálny (alebo minimálny) prvok v množine prvkov, pretože '''tento prvok sa vždy v halde nachádza na vrchu'''. | |||
'''Binárny heap''' je teda strom prvkov (hierarchia), v ktorom je ako koreň vždy '''najväčší''' ('''''max-heap''''') alebo '''najmenší''' ('''''min-heap''''') prvok. Ak pridáme alebo odoberieme nejaký prvok, vlastnosti haldy sa postarajú o to, aby bol na vrchu vždy najväčší prvok. | |||
Haldu môžeme reprezentovať aj lineárne, ako pole prvkov, ak sú splnené nasledovné podmienky: | |||
* Najväčší (v ''max-heap'') alebo najmenší (v ''min-heap'') prvok je v poli '''vždy prvý'''; | |||
* Potomkovia akéhokoľvek rodiča sú v '''''min-heap''''' vždy '''väčší''' ako rodič (alebo '''menší''', v '''''max-heap'''''); | |||
* Musí to byť binárna štruktúra, to znamená že každý rodič musí mať '''práve dvoch''' alebo '''žiadneho''' potomka; | |||
Ďalej platí, že: | |||
* '''Ľavý potomok''' prvku s indexom <math>i</math> sa nachádza na indexe <math>(2 \times i) + 1</math>; | |||
* '''Pravý potomok''' prvku s indexom <math>i</math> sa nachádza na indexe <math>(2 \times i) + 2</math>; | |||
* '''Rodič prvku''' <math>i</math> sa nachádza na indexe <math>\frac{(i - 1)}{2}</math> (zaokrúhlené nadol); | |||
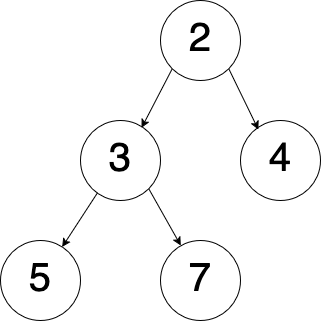
Napríklad, pole <math>\{ 2, 3, 4, 5, 7 \}</math> je ''min-heap'' – rodičom je prvok 2, potomkovia sú 3, 4. 3 má ďalších dvoch potomkov: 5 a 7. Táto halda môže byť vizualizovaná nasledovne: | |||
<div style="display: inline-block; background-color: white;"> | |||
{{#drawio:Príklad min-heap}} | |||
</div> | |||
===== Úlohy pre haldu ===== | |||
Rozhodni, akou haldou sú nasledujúce množiny prvkov: | |||
<quiz display="simple"> | |||
{ <math>\{ 8, 7, 5, 5, 4 \}</math> | |||
|type="()"} | |||
+ max-heap | |||
- min-heap | |||
- nie je halda | |||
{ <math>\{ 2, 4, 7, 9 \}</math> | |||
|type="()"} | |||
- max-heap | |||
+ min-heap | |||
- nie je halda | |||
{ <math>\{ 12, 0, 0, 0, 12 \}</math> | |||
|type="()"} | |||
- max-heap | |||
- min-heap | |||
+ nie je halda | |||
{ <math>\{ 42 \}</math>, je táto množina haldou? | |||
|type="()"} | |||
+ áno | |||
|| Správne! Akákoľvek množina s jedným prvkom spĺňa vlastnosti haldy. | |||
- nie | |||
</quiz> | |||
=== Merge-sort === | |||
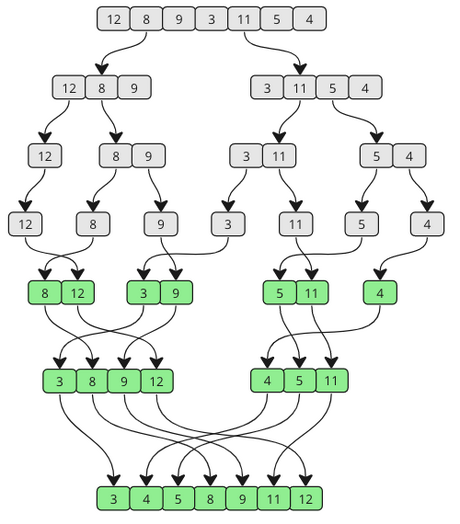
Tento triediaci algoritmus postupne rozbíja pole prvkov na menšie a menšie polovice. Ak sa všetko rozbije iba na jednoprvkové pole, tak sa pokračuje odzadu a prvky sa zoradia postupným zlučovaním, čo vytvorí kompletnú usporiadanú množinu. | |||
[[Súbor:Merge sort.png|alt=Merge sort (zdroj: https://www.w3schools.com/dsa/dsa_algo_mergesort.php)|stred|náhľad|524x524bod|Vizualizácia merge-sortu (zdroj: [https://www.w3schools.com/dsa/dsa_algo_mergesort.php W3Schools])]] | |||
Merge-sort je algoritmus typu '''divide-and-conquer''' (''rozdeľuj a panuj''). Problém triedenia sa rozdelí na menšie problémy ktoré sa riešia individuálne a nakoniec sa iba spoja do súvislého riešenia (tento a ďalší typ algoritmov si vysvetlíme neskôr). | |||
Implementácia merge-sortu v programovacom jazyku Python: | |||
<iframe frameborder="0" style="width: 100%" height="645" src="https://coding.poznamkovac.eu/?lang=sk#/embed/python/algoritmy/triedenie/3"></iframe> | |||
Časová výpočtová zložitosť tohto algoritmu je <math>O(n \times log_2 n)</math>, a toto sa v podstate nemení aj napriek rôznorodosti vstupných dát (algoritmus potrebuje pole rozdeliť vždy rovnako, bez ohľadu na to či je už usporiadané alebo je tam úplný chaos). | |||
{{Téma|Oblast=Kategória:Algoritmy a výpočtová zložitosť|Poradie=60}} | {{Téma|Oblast=Kategória:Algoritmy a výpočtová zložitosť|Poradie=60}} | ||
[[Kategória:Algoritmy a výpočtová zložitosť]] | [[Kategória:Algoritmy a výpočtová zložitosť]] | ||
Aktuálna revízia z 16:17, 20. apríl 2025
Triediace algoritmy Bubble-sort, Selection-sort, Insertion-sort, Quick-sort, Radix-sort, Counting-sort, Heap-sort, Merge-sort, pojmy inverzia, stabilný (triediaci) algoritmus a heap (halda).
Triediace algoritmy
Častým problémom v algoritmizácií je efektívne (rýchle a pamäťovo nenáročné) triedenie množiny údajov, hľadanie najväčšieho a najmenšieho čísla (respektíve, maximálnej a minimálnej hodnoty), hľadanie mediánu (prostrednej hodnoty) a modusu (hodnoty s najčastejším výskytom) a podobne.
Majme napríklad množinu čísiel: . Ako naprogramovať algoritmus ktorý takúto množinu usporiada od najmenšieho čísla po najväčšie? Touto otázkou sa zaoberali už tvorcovia algoritmov pred nami, a v súčasnosti existuje hneď niekoľko algoritmov. Každý algoritmus má svoju výpočtovú zložitosť – niektoré sú efektívnejšie pri menšom počte vstupných hodnôt, iné sú zamerané pre triedenie veľkého množstva hodnôt. Neexistuje teda definitívna odpoveď na to, ktorý algoritmus je najlepší (ale samozrejme vo všeobecnosti vždy hľadáme algoritmus s najmenšou zložitosťou, či už časovou alebo pamäťovou).
V príklade vyššie sú uvedené čísla, ale samozrejme triedenie môžeme realizovať nad všetkým, čomu rozumieme že má nejakú postupnosť (napríklad: abecedný zoznam, zoradiť veľkosti objektov od najväčšieho po najmenší, usporiadanie farebného spektra, triedenie dátumov, postupnosť dní v týždni, knižné kapitoly a podobne). Neexistuje algoritmus ktorý dokáže realizovať triedenie súčasne na všetkých možných množinách prvkov (napríklad, usporiadanie písmen na klávesnici je iné ako abecedná postupnosť tých istých písmen), preto tieto algoritmy väčšinou prispôsobujeme našim potrebám.
Bubble-sort
Za asi najznámejší triediaci algoritmus sa považuje Bubble-sort ("bublinové triedenie"). Z implementačného hľadiska je to vcelku jednoduchý algoritmus, ktorého princíp spočíva v postupnej výmene prvkov s nesprávnym poradím, pričom každý prvok "vybublá" na správne miesto.
V príklade vyššie je na vstupe pole s 5 číslami. Algoritmus bubble sort obsahuje dva vnorené cykly:
- Vonkajší cyklus zabezpečuje prechod od posledného indexu poľa k prvému. Je to preto, že s každou iteráciou v tomto cykle je garantované, že sa usporiada práve jedno číslo ("vybublá", preto sa tento algoritmus nazýva bubble-sort). Je zbytočné kontrolovať čísla, ktoré už boli správne vytriedené – preto tento cyklus začína od konca a
isa s každou iteráciou znižuje. - Vonkajší cyklus je ten, ktorý realizuje triedenie (porovnávanie dvoch susedných prvkov). Ak je prvý prvok väčší ako prvok ktorý nasleduje, tak sa vymenia. S každou iteráciou sa najväčšie prvky budú posúvať doprava, takže pole bude zoradené od najmenšieho po najväčší (vzostupne). Ak je potrebné čísla zoradiť naopak (od najväčšieho po najmenší, teda zostupne), tak stačí obrátiť znak porovnania (zmeniť podmienku na
if pole[j] < pole[j + 1]).
Je to v podstate algoritmus, ktorý posúva maximálne prvky doprava (alebo doľava, ak triedime zostupne), čím sa prvky zotriedia ("vybublajú") na správne miesto.
Algoritmus bubble-sort má časovú výpočtovú zložitosť (v najhoršom prípade), je to jeden z najmenej efektívnych algoritmov. Používame ho napríklad vtedy, keď:
- Triedime menší počet hodnôt a teda takáto výpočtová zložitosť je pre nás akceptovateľná;
- Nevieme naprogramovať niečo lepšie;
Na nasledujúcej úlohe si môžeme skúsiť bubble-sort naprogramovať v Pythone:
Inverzia
Inverzia je dvojica prvkov, ktoré majú zlé poradie (v závislosti od toho, ako by sme chceli aby boli prvky usporiadané).
Napríklad, ak máme množinu čísiel ktorá má byť zoradená od najmenšieho čísla po najväčšie, tak dvojica prvkov má zlé poradie. Teda, môžeme povedať že táto množina má 1 inverziu. Ak by malo byť pole zoradené od najväčšieho čísla po najmenšie, tak toto pole má hneď 9 inverzií (aby bolo pole usporiadané, tak by sme museli spraviť 9 výmien).
Existuje algoritmus, podľa ktorého dokážeme zistiť počet inverzií. Pre pole vyššie by sme postupovali takto (pokiaľ by pole malo byť usporiadané od najväčšieho po najmenší):
- Vyberieme si stranu z ktorej začneme – buď od ľavej strany alebo od pravej. Povedzme, že si vyberieme ľavú. Prvým prvkom v poli zľava je číslo .
- Spočítame, ktoré prvky na pravej strane od 1 sú väčšie ako 1. Sú to štyri čísla: .
- Ak sme vyčerpali všetky čísla, presunieme sa o jedno miesto doľava a zopakujeme postup. Od čísla 3 sú napravo väčšie dve čísla: . Od čísla 2 sú to opäť tie isté dve čísla. Od 4 je väčšie jedno číslo ().
- Nakoniec iba spočítame všetky väčšie čísla napravo od každého čísla (to, čo sme teraz zisťovali). Teda: inverzií.
Ak by sme mali usporiadať pole opačne (od najmenšieho po najväčší), postupovali by sme rovnako – iba s tým rozdielom, že by sme hľadali prvky ktoré sú na pravej strane menšie ako aktuálne číslo.
Inverzie sa vyskytujú vo všetkých štruktúrach ktoré nie sú správne zoradené a od ktorých očakávame nejaké poradie. Môže to byť napríklad abecedný zoznam mien, zoznam objektov ktoré majú byť zoradené podľa veľkosti ale aj postupnosť dní v týždni – všetko, čo má nejaké poradie.
Počet inverzií môžeme zistiť pomocou algoritmu v bubble-sorte tak, že vytvoríme na začiatku premennú ktorá predstavuje počet inverzií (na začiatku má hodnotu
0), a toto počítadlo zvýšime vždy o 1 keď v bubble-sorte vymeníme dva susedné prvky. Po ukončení vonkajšieho cyklu bude táto premenná obsahovať počet inverzií pre dané pole.Úlohy pre určenie počtu inverzií
Selection-sort
Selection-sort (triedenie výberom) algoritmus vyberá z poľa prvkov najmenší prvok a presunie ho na začiatok.
Výpočtová zložitosť tohto algoritmu je . Vo všeobecnosti je rýchlejší ako bubble-sort, avšak pomalší ako insertion-sort.
Insertion-sort
Insertion-sort (triedenie priamym vkladaním) používa jednu časť triedeného poľa pre ukladanie už vytriedených hodnôt a druhú časť toho istého poľa pre hodnoty ktoré ešte nemajú správne poradie. Princíp je podobný ako pri selection-sorte.
Časová výpočtová zložitosť je . Avšak narozdiel od selection-sortu, rýchlosť insertion-sortu závisí od vstupného poľa – pre takmer utriedené pole prebehne veľmi rýchlo.
Quick-sort
Ako už napovedá názov, quick-sort je jeden z najrýchlejších triediacich algoritmov. Quick-sort funguje vo všeobecnosti takto:
- Z poľa hodnôt sa vyberie jeden prvok ako pivot;
- Zvyšok poľa sa zoradí tak, že hodnoty menšie ako pivot budú naľavo od neho a hodnoty väčšie ako pivot budú napravo;
- Pivot sa vymení s prvým prvkom v podmnožine s väčšími hodnotami tak, aby pivot spadol medzi menšie a väčšie hodnoty – to rozdelí pôvodné pole na dve podmnožiny, kde menšie prvky sú naľavo a väčšie napravo;
- Celý postup sa rekurzívne opakuje pre obe podmnožiny menších prvkov naľavo a väčších prvkov napravo. Ak nezostane žiadna podmnožina pre ďalšie triedenie, pole je zoradené a rekurzia sa ukončí (triviálny prípad).
Implementácia quick-sortu je komplexnejšia, preto pripájam už hotový algoritmus v Pythone:
Časová výpočtová zložitosť algoritmu quick-sort je v najhoršom prípade , avšak v priemernom prípade je to iba , preto je v priemere oveľa efektívnejší ako ostatné algoritmy a patrí medzi najrýchlejšie triediace algoritmy.
Radix-sort
Radix-sort je triediaci algoritmus, ktorý triedi väčšie číselné hodnoty na základe ich cifier, začína od najmenej významnej číslice (sprava doľava). Radix predstavuje základ čísla – v našej (desiatkovej) číselnej sústave máme 10 číslic: od 0 po 9.
Výpočtová zložitosť tohto algoritmu sa dá všeobecne uviesť ako , kde je počet hodnôt ktoré sa majú vytriediť a predstavuje počet cifier v najväčšej hodnote (z ). Najlepším prípadom je ten, keď má tento algoritmus veľa hodnôt pre triedenie ale všetky hodnoty majú nízky počet číslic (napríklad, triedenie 1 milióna hodnôt ktoré majú rozsah 0 – 999, teda maximálne 3 cifry). V takýchto prípadoch sa časová výpočtová zložitosť môže zjednodušiť iba ako .
Radix-sort je algoritmus, ktorý by pre správne fungovanie mal byť naprogramovaný ako stabilný.
Stabilita triediaceho algoritmu
Algoritmus triedenia sa považuje za stabilný, ak sa po zoradení zachová relatívne poradie rovnakých prvkov. Nestabilný algoritmus zachovanie tohto poradia negarantuje.
Povedzme napríklad, že máme zoznam písmen abecedy ktoré obsahujú určitú hodnotu (môže to byť napríklad počet ľudí ktorí považujú toto písmeno za ich obľúbené). Chceme tento zoznam zoradiť od najobľúbenejšieho písmena po najmenej obľúbené. Ak majú dve susedné písmená rovnakú obľúbenosť, zoradíme ich podľa ich abecedného poradia.
Majme napríklad písmená "K" a "L", pričom obidve majú hodnotu 240. Stabilný algoritmus správne zoradí písmená ako "K" a za ním bude nasledovať "L", avšak nestabilný algoritmus (ktorý triedi iba na základe obľúbenosti a neberie ohľad na abecednú postupnosť) by ich mohol zoradiť ako "L" a "K", čo je avšak nesprávne pretože nie je zachovaná relatívna postupnosť prvkov (na základe obľúbenosti ako primárneho zoradenia) a takýto algoritmus je nestabilný.
Counting-sort
Tento algoritmus usporiada prvky v množine tak, že spočíta koľkokrát sa tam daný prvok nachádza. Je to užitočné, ak máme veľa opakujúcich sa hodnôt a malú rôznorodosť dát. V najhoršom prípade má výpočtovú zložitosť .
Heap-sort
Heap-sort (haldové triedenie) je triediaci algoritmus, ktorý využíva heap (haldu) pre efektívne triedenie prvkov. Je vnímaný ako optimalizácia selection-sortu, pretože heap nám umožní rýchlo nájsť v poli minimálnu (alebo maximálnu) hodnotu pre zámenu v čase namiesto . V dôsledku toho má tento algoritmus celkovú výpočtovú zložitosť .
Heap (halda)
Heap (halda) je dátová štruktúra, ktorá spĺňa vlastnosti heapu (haldy). Je vhodná pre prípady keď potrebujeme častokrát uchovávať maximálny (alebo minimálny) prvok v množine prvkov, pretože tento prvok sa vždy v halde nachádza na vrchu.
Binárny heap je teda strom prvkov (hierarchia), v ktorom je ako koreň vždy najväčší (max-heap) alebo najmenší (min-heap) prvok. Ak pridáme alebo odoberieme nejaký prvok, vlastnosti haldy sa postarajú o to, aby bol na vrchu vždy najväčší prvok.
Haldu môžeme reprezentovať aj lineárne, ako pole prvkov, ak sú splnené nasledovné podmienky:
- Najväčší (v max-heap) alebo najmenší (v min-heap) prvok je v poli vždy prvý;
- Potomkovia akéhokoľvek rodiča sú v min-heap vždy väčší ako rodič (alebo menší, v max-heap);
- Musí to byť binárna štruktúra, to znamená že každý rodič musí mať práve dvoch alebo žiadneho potomka;
Ďalej platí, že:
- Ľavý potomok prvku s indexom sa nachádza na indexe ;
- Pravý potomok prvku s indexom sa nachádza na indexe ;
- Rodič prvku sa nachádza na indexe (zaokrúhlené nadol);
Napríklad, pole je min-heap – rodičom je prvok 2, potomkovia sú 3, 4. 3 má ďalších dvoch potomkov: 5 a 7. Táto halda môže byť vizualizovaná nasledovne:
Úlohy pre haldu
Rozhodni, akou haldou sú nasledujúce množiny prvkov:
Merge-sort
Tento triediaci algoritmus postupne rozbíja pole prvkov na menšie a menšie polovice. Ak sa všetko rozbije iba na jednoprvkové pole, tak sa pokračuje odzadu a prvky sa zoradia postupným zlučovaním, čo vytvorí kompletnú usporiadanú množinu.
Merge-sort je algoritmus typu divide-and-conquer (rozdeľuj a panuj). Problém triedenia sa rozdelí na menšie problémy ktoré sa riešia individuálne a nakoniec sa iba spoja do súvislého riešenia (tento a ďalší typ algoritmov si vysvetlíme neskôr).
Implementácia merge-sortu v programovacom jazyku Python:
Časová výpočtová zložitosť tohto algoritmu je , a toto sa v podstate nemení aj napriek rôznorodosti vstupných dát (algoritmus potrebuje pole rozdeliť vždy rovnako, bez ohľadu na to či je už usporiadané alebo je tam úplný chaos).